A five - letter code is formed by selecting 5 different letters from the 12 letters A, B, C, D, E, F, G, H, I, J, K, and L and placing these 5 letters in the 5 spaces shown in Figure. Which of the following expressions is the number of different five - letter codes that are possible ?
A
12!4!8!
B
12!(5!)(7!)
C
12!7!
D
12!5!
Video Solution
Text Solution
The correct Answer is:C
The number of five - letter codes possible is the number of ways of permuting 5 different objects from 12 different objects. Say that .nPk is the number of ways to permute k different objects from n different object, where n is a positive integer and k is an integer such that 0≤kn. Then .nPk=n!(n−k)!. In this question, n = 12 and k =5. The number of possible five - letter codes is 12!(12−5)!=12!7!
You can solve the question in this way also : Call the space furthest to the left space I , the space adjacent to the space furthest to the left space II , the space in the center space III , the space adjacent to the space furthest to the right space IV , and the space furthest to the right space V. You can place any of the 12 letters in space I. For each of these 12 letters in space I, you can place 12−1=11 letters in space II. For any pair of letters in spaces I and II, you can place 12−2=10 letters in space III. For any triplet of lettes in space IV. For any set of 4 letters in spaces I, II, III and IV, you can place 8 letters in space V. The number of possible five - letter codes is (12)(11)(10)(9)(8). This can be rewritten as (12)(11)(10)(9)(8)7!7! which equals 12!7! matching (C ).
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
License plates on cars in a certain state consist of 3 letters taken from the 26 letters. A through Z, followed by 3 digits taken from the 10 digits, 0 through 9. Which of the following expressions gives the number of distinct license plates that are possible given that repetition of both letters and digits is allowed?
A103⋅263B(10+26)3C2(26!)3(10!)3D(3+3)26+10Select correct answers from the choices A, B, C, D which are given. Write down only the letter corresponding to the correct answer.
Which of the following oxides is amphoteric?AZnOBCuOCFeODCaOSelect the letter will replace the question mark (?) in the following series.
K, Q, V,?, C, E, FAYBACXDZ
Describe the following wets in Roster form: The set off all letters in the word 'ALGEBRA'
View SolutionFind the number of ways in which the letters A, B, C, D, E, F can be placed in the 8 boxes of the given figure so that no row remains empty. (figure)
View SolutionDescribe the following wets in Roster form: The set off all letters in the word 'MATHEMATICS'
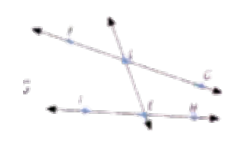
View SolutionIn the given figure . Which of the following are non collinear points ?
L and E
(b) F.L and G
( c ) I. E and H
(d) F.L and E
View SolutionThe five number 1056, 1098, 1100 and 1126 are represented on a number line by the point A, B, C, D and E, respectively, as shown in the figure. Which one of the following points represents the average of the five numbers ?
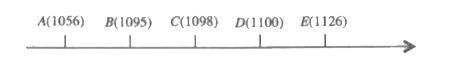
View Solution
