A fruit grower canuse two types of fertilizer in his garden brand P and brand Q. The amounts (in kg) of nitrogen phosphoric acid, potash, and chlorine a bag of each brand are given in the stable. Tests indicate that the garden needs at least 240kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
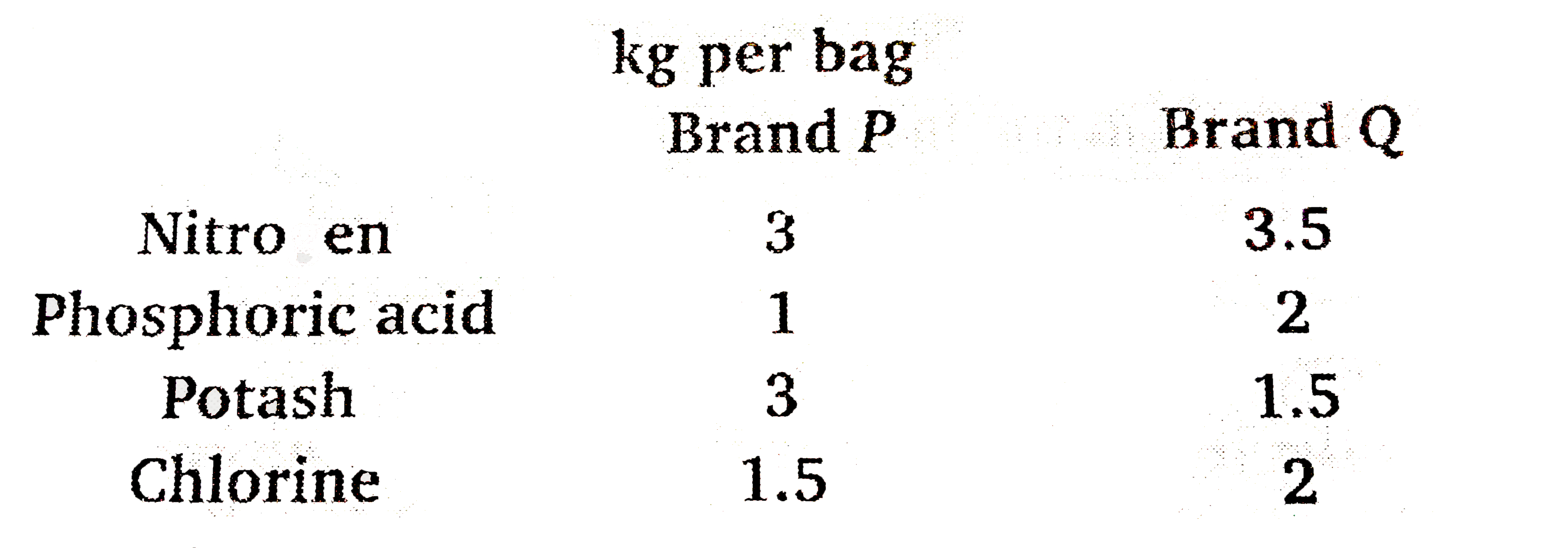
Let x bags of brand P and y of brand Q are used by fruit grower.
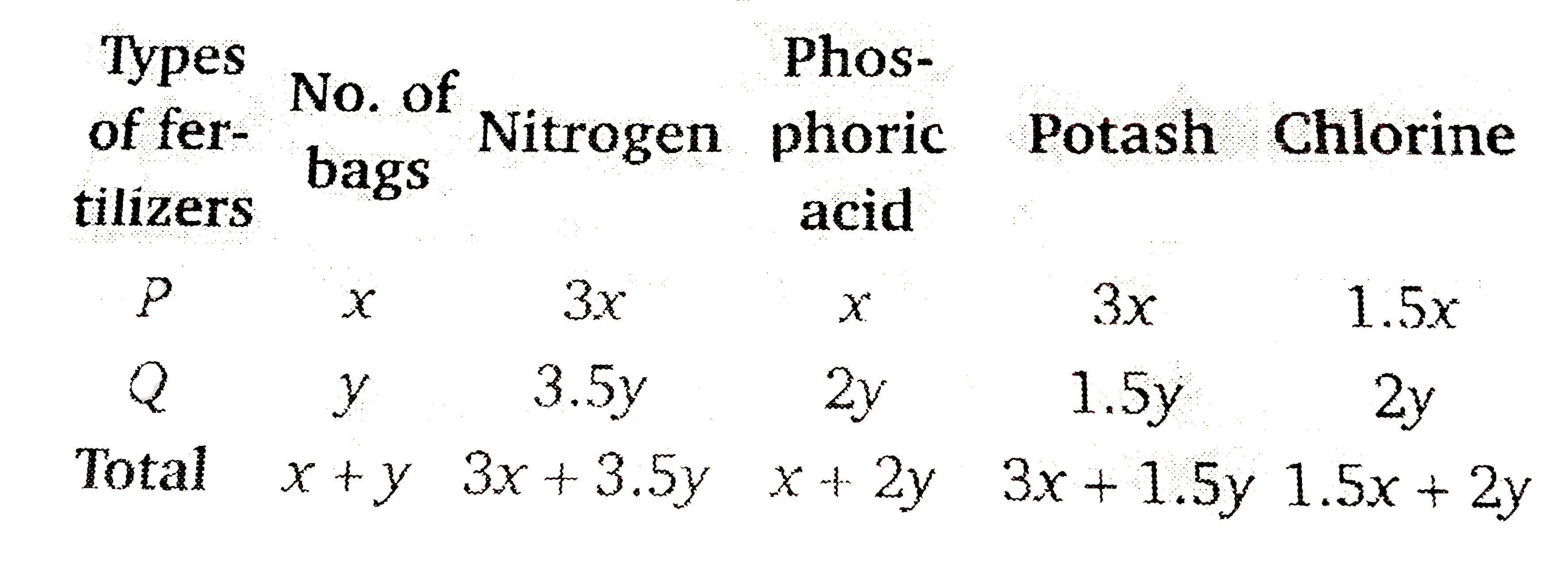
Minimise Z=3x+3.5y……………1
and constraints x+2y≥240………………2
3x+1.5y≥270………………….3
1.5x+27≤310……………..4
x≥0,y≥0.......................5
First draw the graph of the line x+2y=240

Put (0,0) in the inequation x+2y≥240
0+2×0≥240⇒0≥240 (False)
Thus, the half plane does not contain origin.
Now, draw the graph of the line 3x+1.5y=270
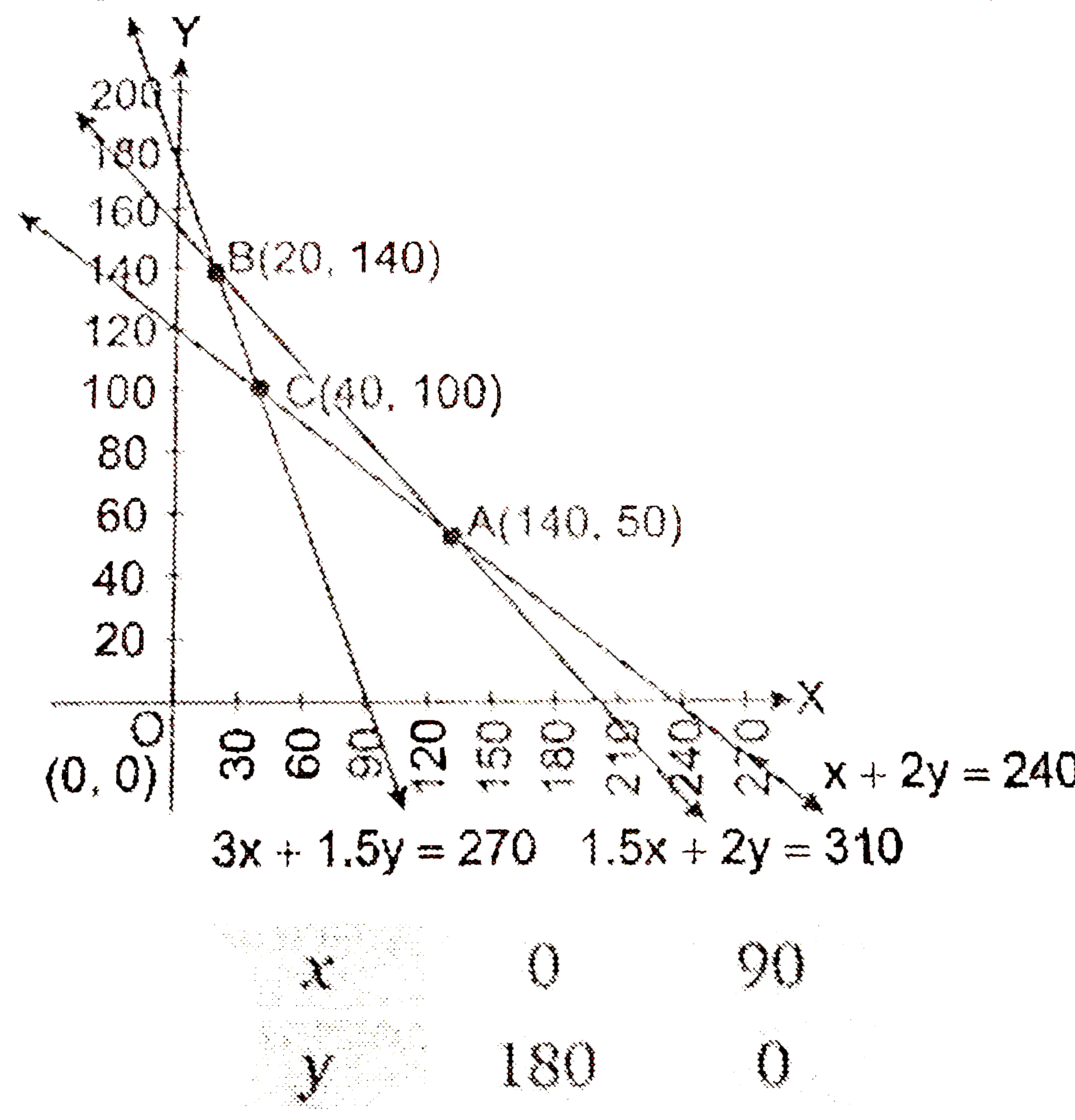
Put (0,0) in the inequations 3x+1.5y≥270
3×0+1.5×0≥270⇒0≥270 (False)
Thus, the half plane does not contain origin.
Now, draw the graph of the line 1.5x+2y=310
PUt (0,0) in the inequation 1.5x+2y≤310
1.5×0+2×0≤310⇒0≤310 (True)
Thus, the half plane does not contain origin.
Since x,y≥0
So the feasible region will be in first quadrant.
The point of intersection of equations 1.5x+2y=310 and x+2y=240 is A(140,50). Similarly the point of intersection of the equation 3x+1.5y=270 and 1.5x+2y=310 is B(20,140).
∴ Feasible region is ABCA.
It vertices are A(140,50),B(20,140) and C(40,100) at which we find the value of Z.

Therefore, the minimum value of Z is 470 at point C(40,100). Minimum nitrogen to be mixed in garden is 470 kg for which 40 bags of brand P and 100 bats of brand Q should be used.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.2
11 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine m a bag of each brand are given m the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
View SolutionRefer to Question 8. If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?
View SolutionThere are two types of fertilisers F1and F2. F1, consists of 10% nitrogen and 6% phosphoric acid and F2consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a fanner finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 cost Rs.6/kg and F2 costs Rs.5/kg, determine how much of each type of fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
View SolutionLeast stable oxide of chlorine is:
View SolutionFruit growers grow two or more varieties of fruits in their orchards to have
View SolutionA gardener has a supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used, so that nutrient requirements are met at a minimum cost. What is the minimum cost?
View SolutionThere are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs Rs. 10 per kg and ‘B’ cost Rs. 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirement are met at a minimum cost.
View SolutionThere are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs Rs. 10 per kg and ‘B’ cost Rs. 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirement are met at a minimum cost.
View SolutionThere are two types of fertilisers F1 and F2.F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing he soil conditions a farmer finds that she needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs Rs. 6/kg and F2 costs Rs. 5/kg, determine how much of each type of fertiliser should be used to that nutrient requirements are met at a minimum cost. What is the minimum cost?
View SolutionThere are two types of fertilizers F1 and F2.F1 consists of 10% nitrogen and 6% phosphoric acid and F2 contains 5% nitrogen and 10% phosphoric acid. After testing the soil condition a farmer finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid forhis crop. If F1 costs Rs. 6 per kg and F2 costs Rs. 5 perkg, determine how muchofeach of fertilizers beused so that nutrient requirements are met at a minimum cost. What is the minimum cost?
View Solution
