A liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
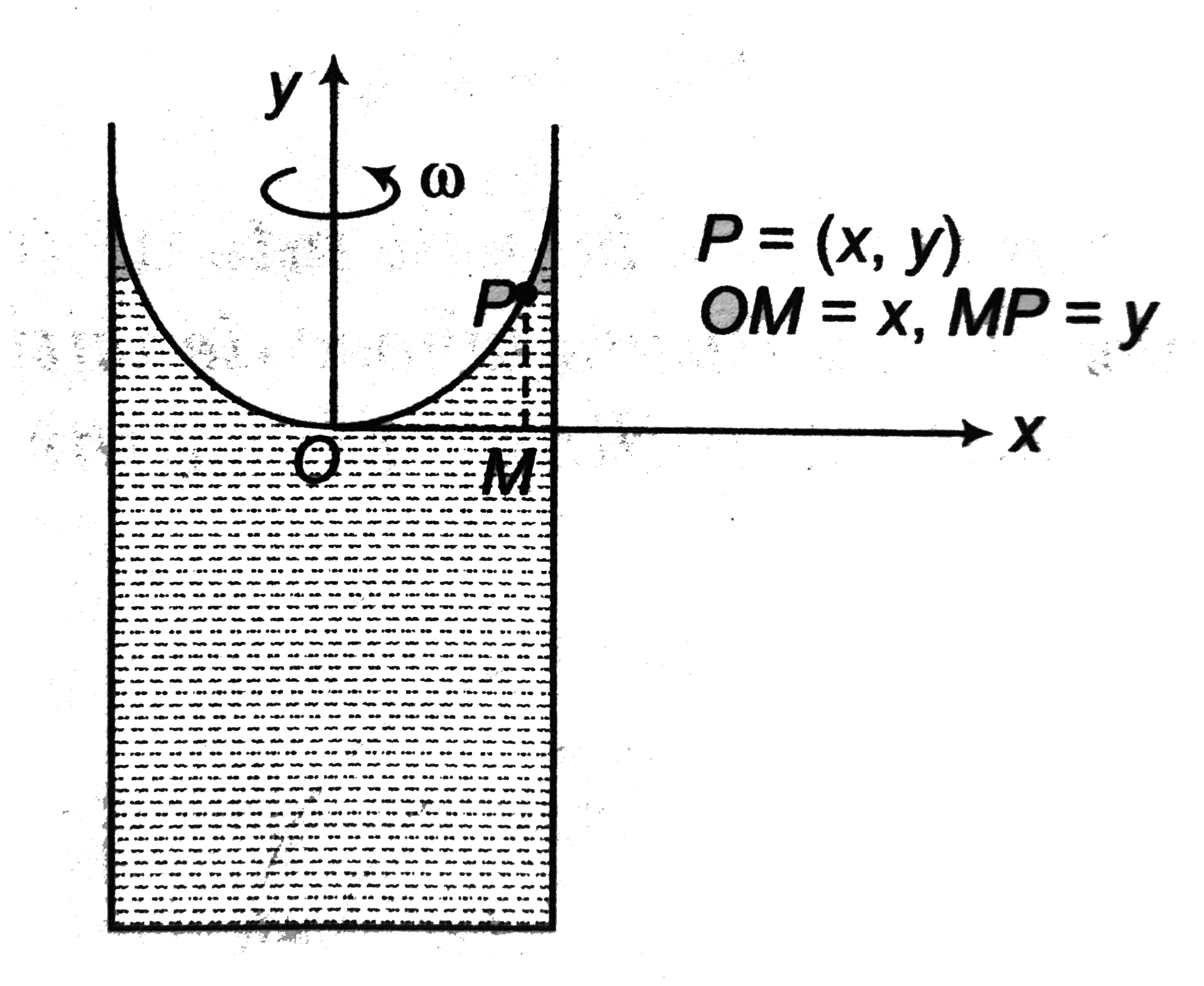 .
.
Writing pressure equation along the path PMO.
pP+ρgy−ρω2x22=po
Points Pand Oare open to atmosphere.
so, pressure at these point are same(= atmospheric pressure).Therefore, the above equation becomes,
ρgy−ρω2x22=0 or,y=(ω22g)(x2)
This is the required parabolic equation of free surface of liquid.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.16videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions

A liquid of density ρ is rotated by an angular speed ω as shown in figure, Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
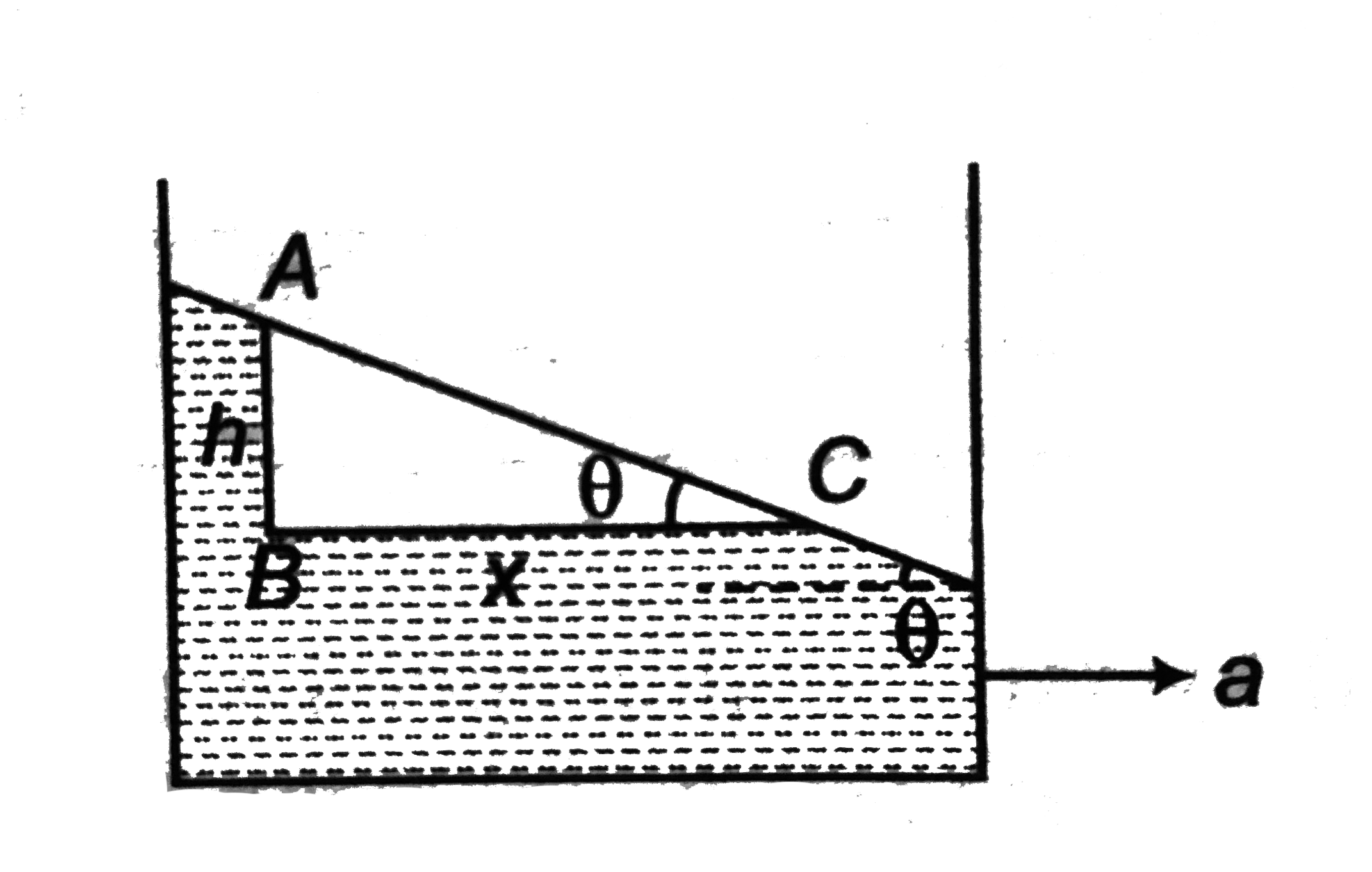
Using the pressure equation along the path ABC find the angle θ.View Solution
Knowledge Check
- Question 1 - Select One
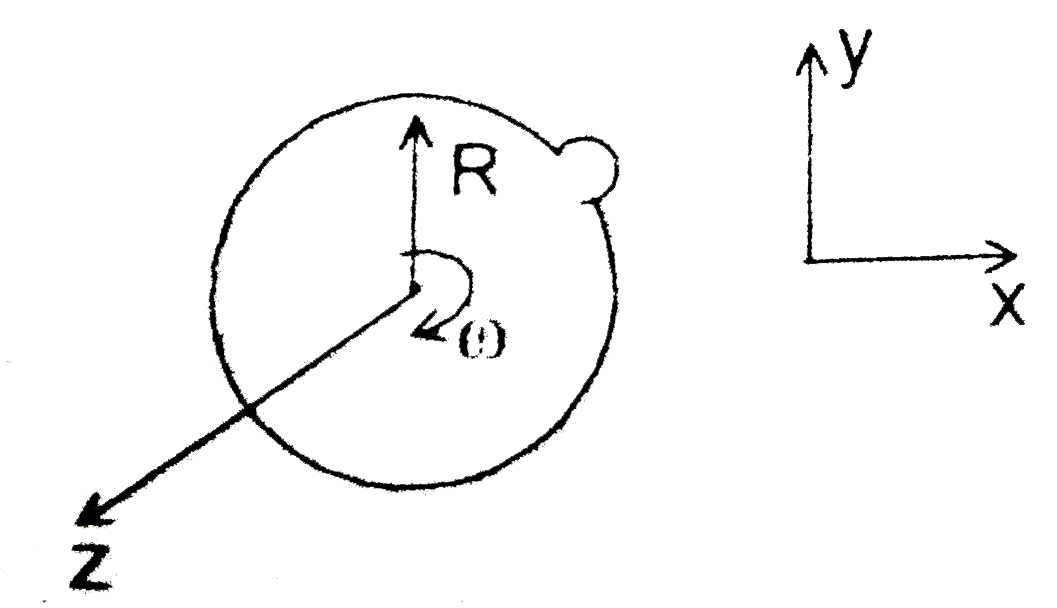
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.AωRBωR/2C2ωRDzero - Question 2 - Select One
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
AhBaCρDg - Question 3 - Select One
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
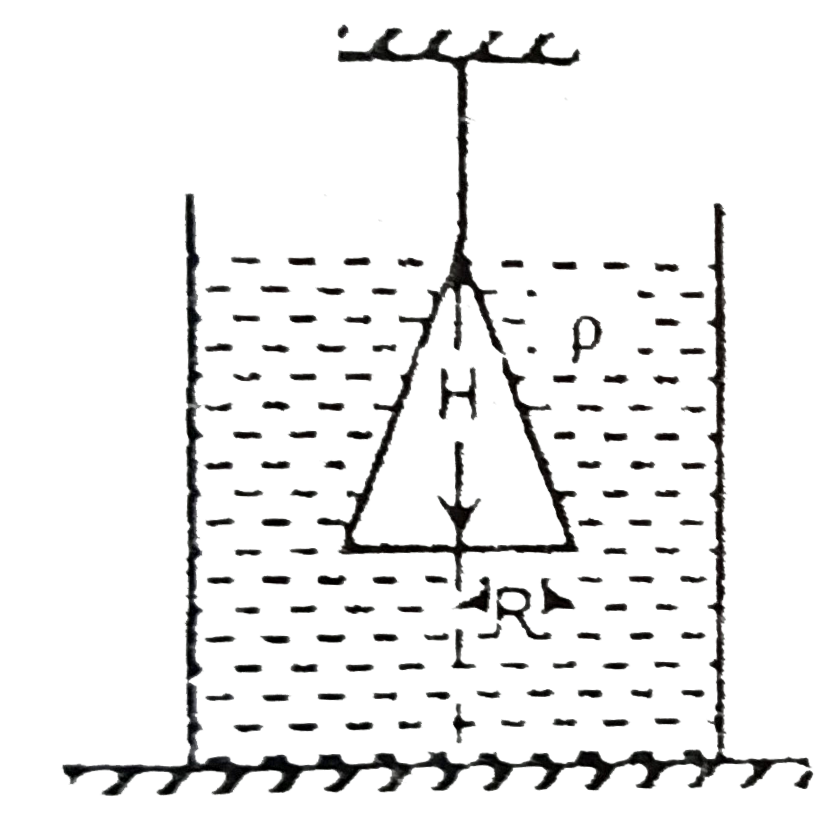 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
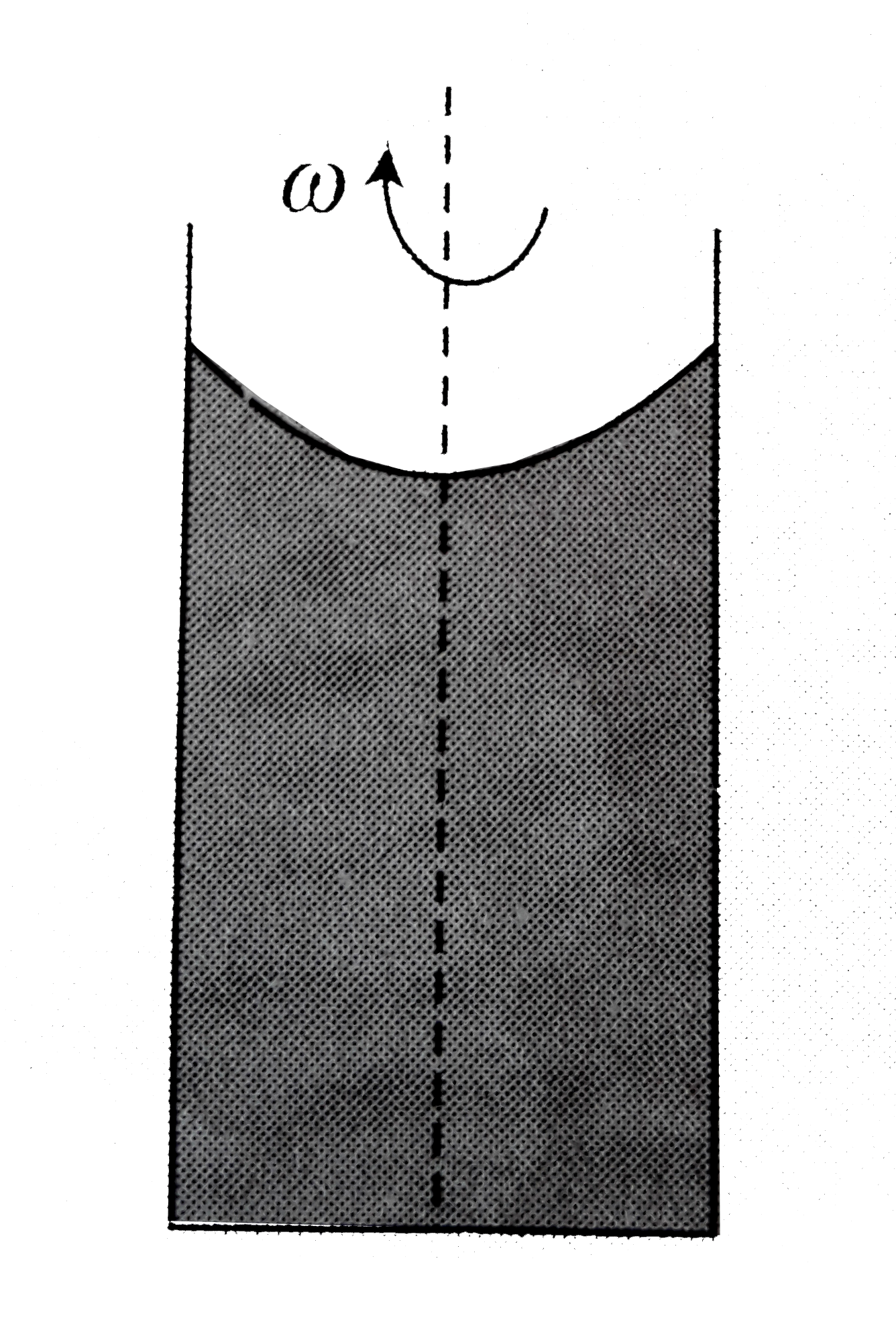
A liquid of density ρ is in a bucket that spins with angular velocity 'ω' as shown in figure. Prove that the free surface of the liquid has a parabolic shape. Find equation of this.
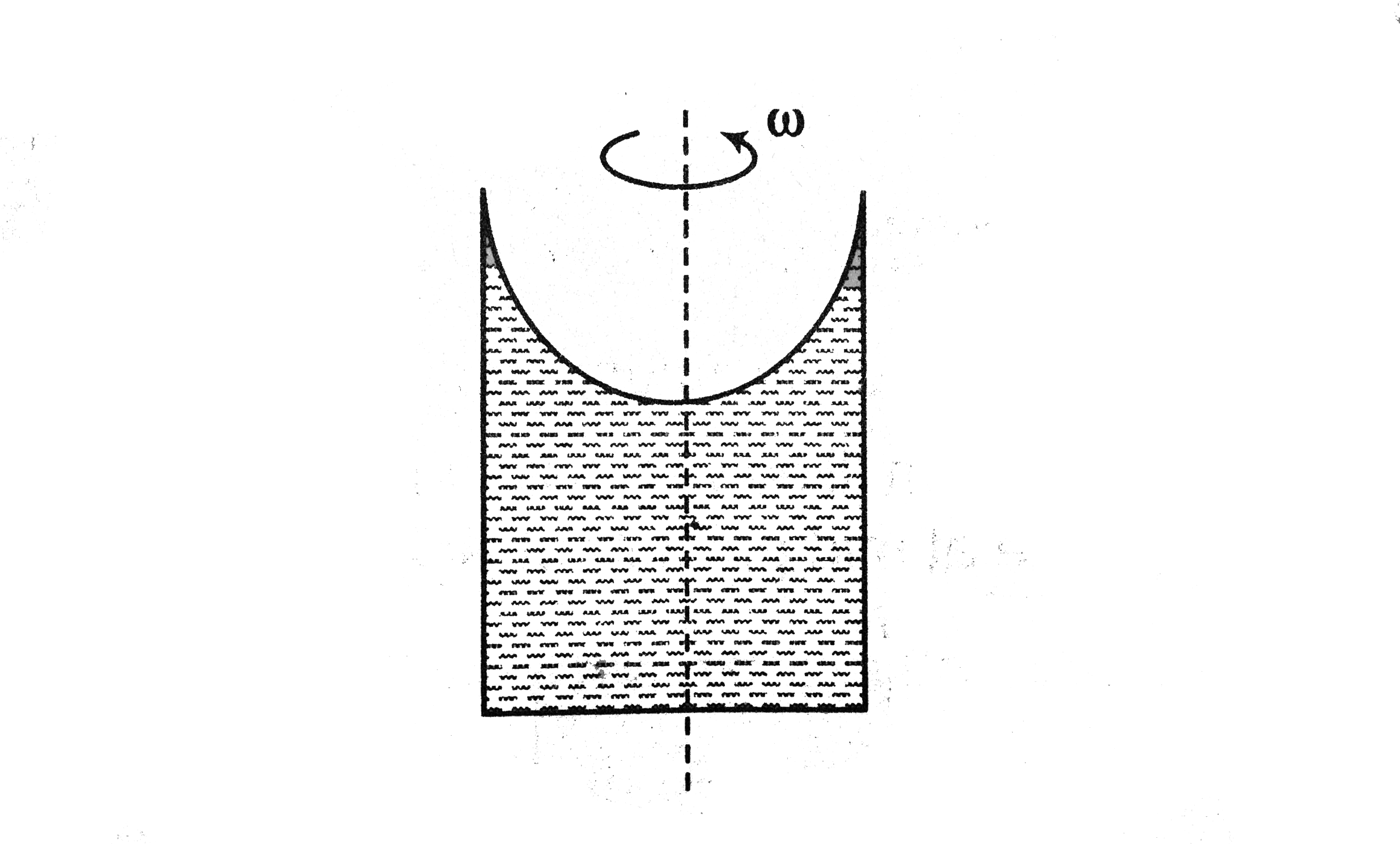 .View Solution
.View SolutionA liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .View Solution
.View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
 View Solution
View SolutionA liquid of density ρ has to spray with help of aspirator pump at height H from liquid level as shown in figure. If gauge pressure inside bulb is P and density of air is σ then velocity of air in tube AB is
 View Solution
View Solution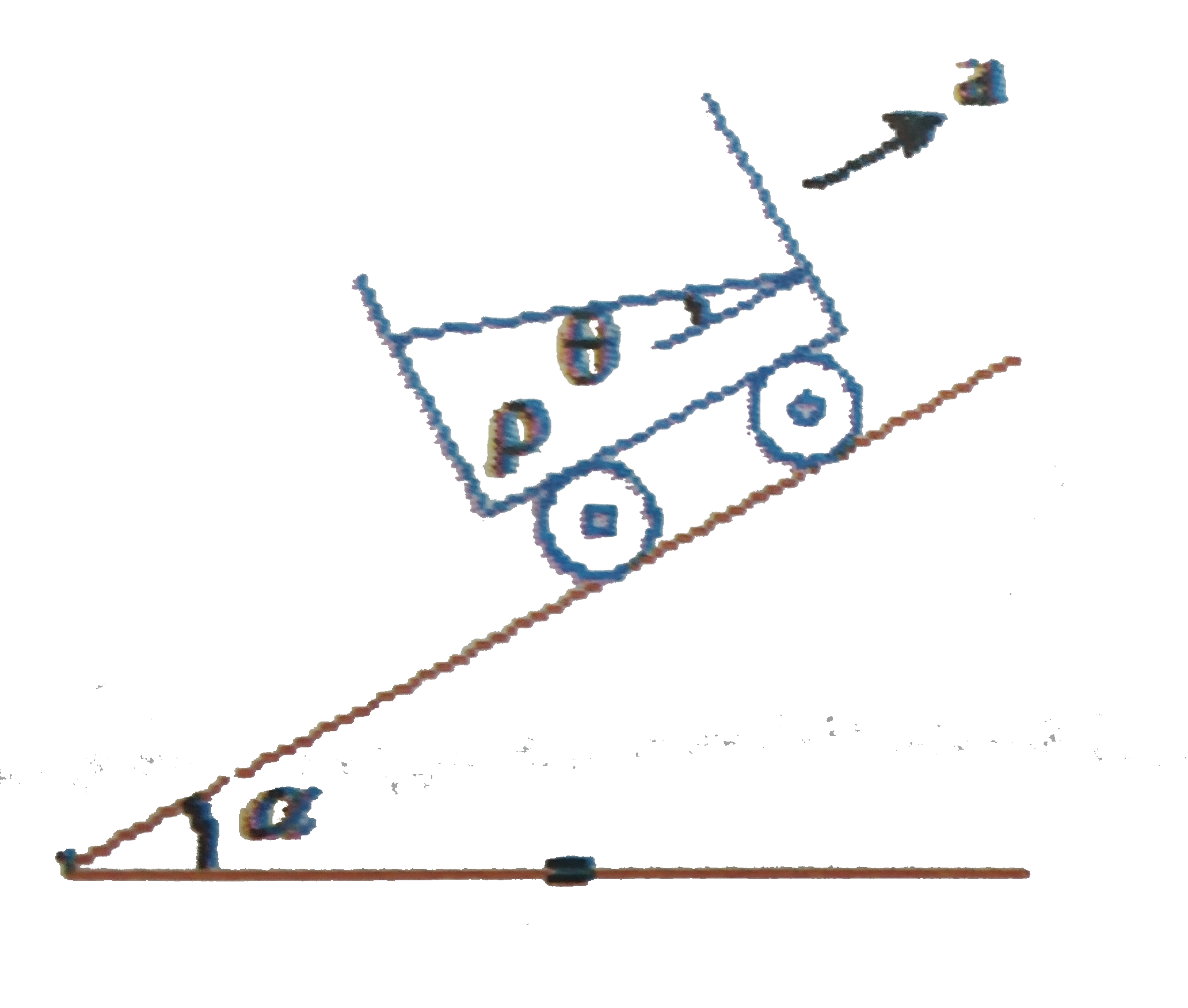
A fluid container is containing a liquid of density ρ is accelerating upward with acceleration a along the inclined plane of inclination α as shown in the figure. Then the angle of inclination θ of free surface isView Solution

