A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs.17.50 per package on nuts and Rs.7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at the most 12 hours a day? Form the linear programming problem and solve it graphically.
Let x packets of nuts and y packets of bolts produced in one day. Then
Maximize : z=10x+5y
Subject to: x≥0
y≥0
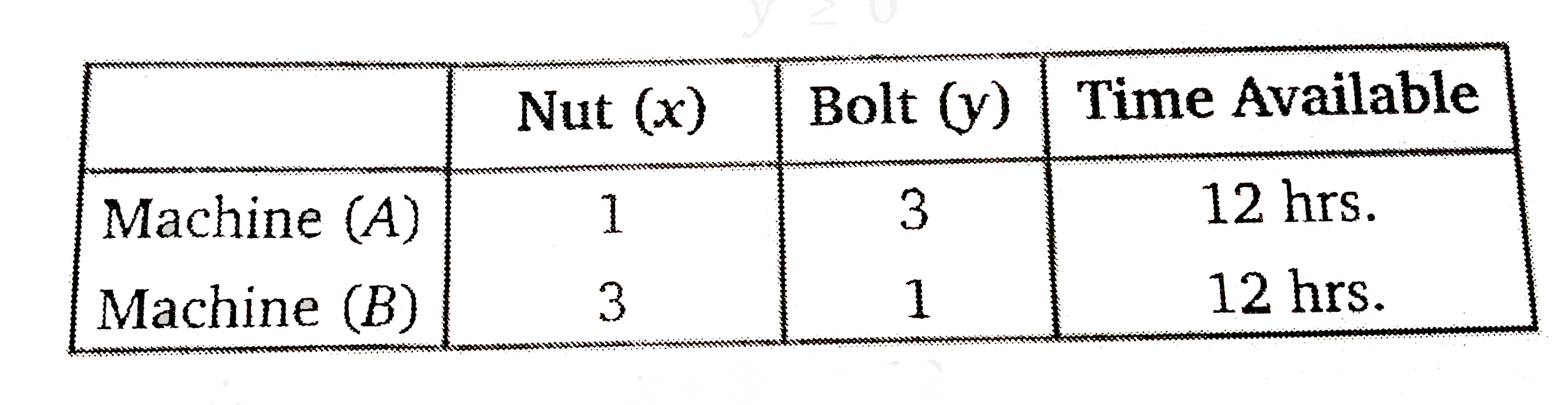
x+3y≤12
3x+y≤12
Draw the graph of the equations x=0,y=0,x+3y=12 and 3x+y=12.
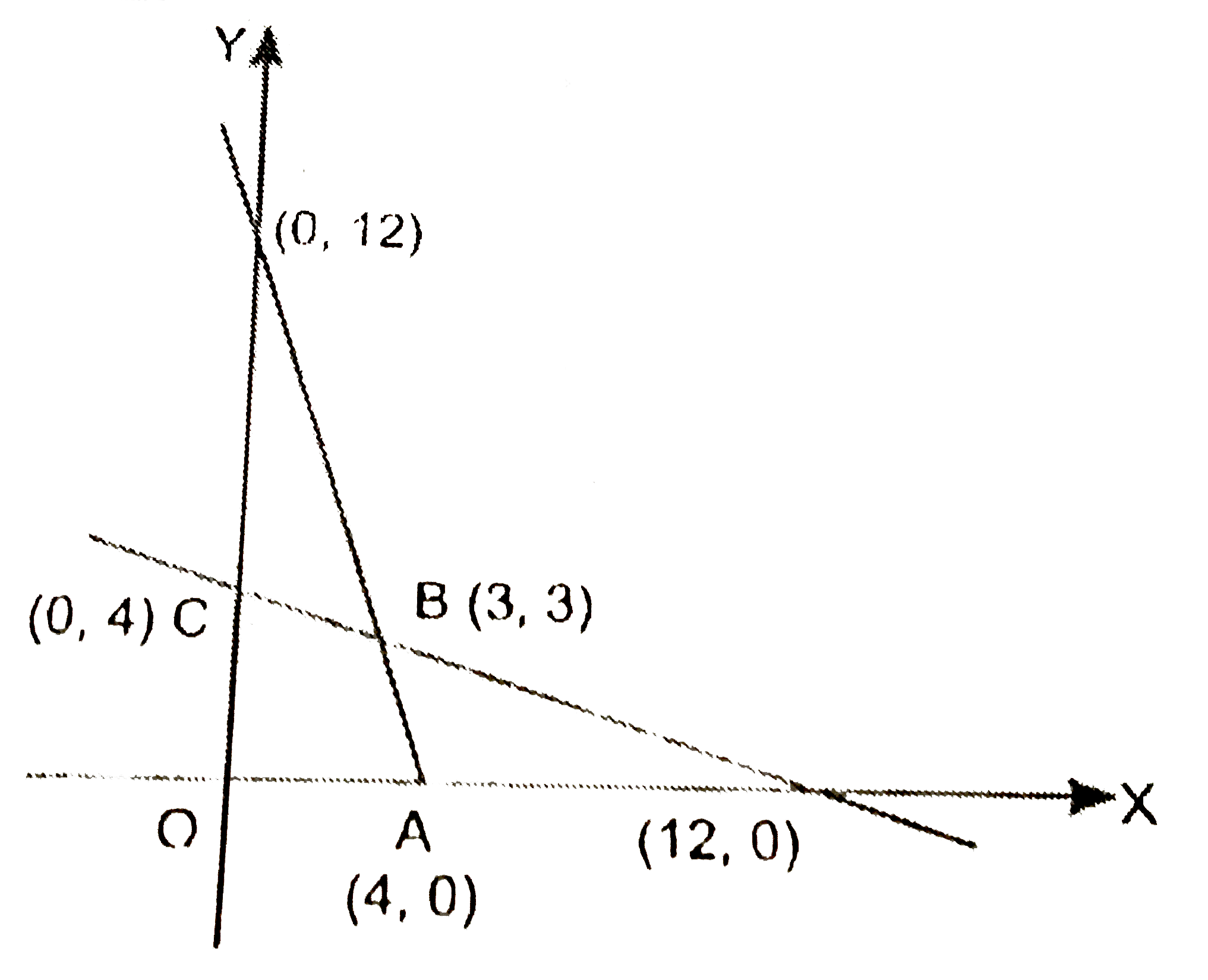
Now obtain the feasible region for the inequations x≥0,y≥0,x+3y≤12 and 3x+y≤12 and shade it. The convex region is OABC whose vertices are O(0,0),A(4,0),B(3,3) and C(0,4). We will find the value of z=10x+54y at these vertices.
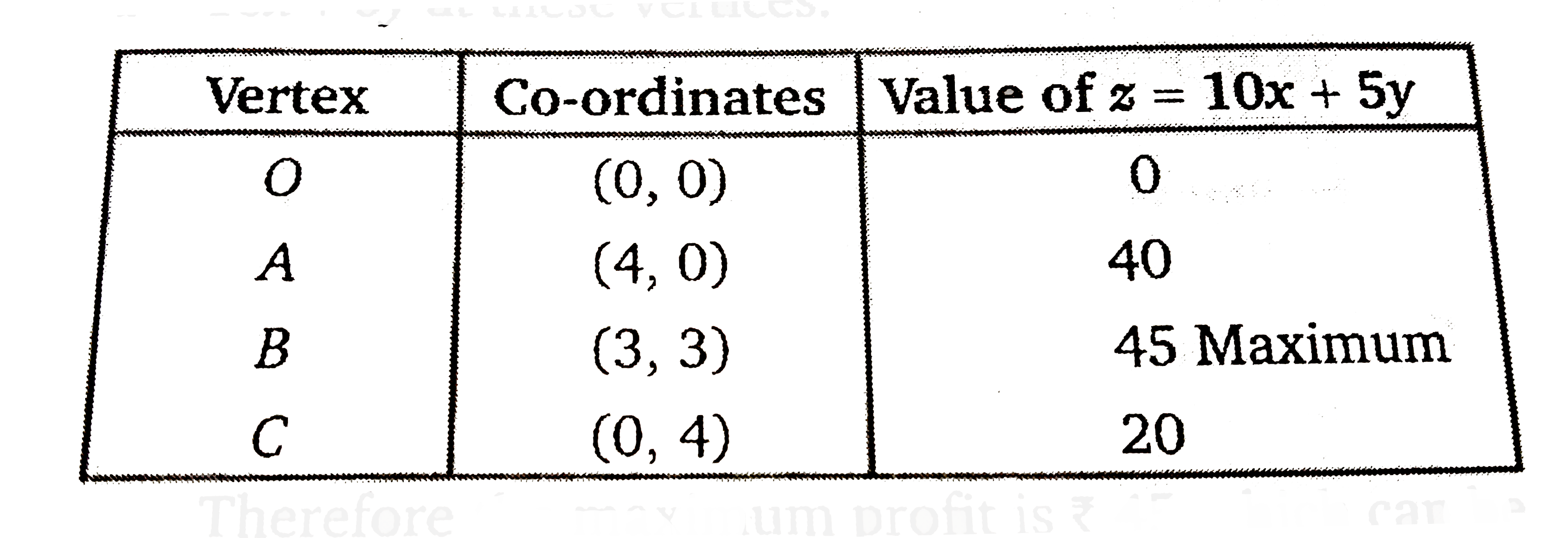
Therefore the maximum profit is Rs. 45 which can be obtained by producing 3 packets of nuts and 3 packets of bolts.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A
8 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B
17 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rsl7.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View Solution
Knowledge Check
A firm makes pants and shirts . A shirt takes 2 hours on machine and 3 hours of man lobour while a pant takes 3 hours on machine and 2 hours of man labour .In a week , there are 70 hours of machine and 75 hous of man lobour available . If the firm dertermines to make x shirts and y pants per week , then for this linear constraints are
Ax≥0,y≥0,2x+3y≥70,3x+2y≥75Bx≥0,y≥0,2x+3y≤70,3x+2y≥75Cx≥0,y≥0,2x+3y≥70,3x+2y≤75Dx≥0,y≥0,2x+3y≤70,3x+2y≤75
A manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View Solution(i) A manufacturer produces nuts and bolts for industrial machinery.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit og ₹ 17.50 per package of nuts and ₹ 7.00 per package of bolts.How many packages of each should be produced each day so as to maiximise his profit, if he operate his machine for at the most 12 hous a day?Form an LPP for the problem and solve it graphically.
(ii) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on amchine A and 1 hour on machine B to produce a package of bolts.He earns a profit ₹35 per package of nuts and ₹14 per package of bolts.How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day? Convert it into an LPP and solve graphically.
View Solution(i) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit og ₹ 17.50 per package of nuts and ₹ 7.00 per package of bolts.How many packages of each should be produced each day so as to maiximise his profit, if he operate his machine for at the most 12 hous a day?Form an LPP for the problem and solve it graphically.
(ii) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on amchine A and 1 hour on machine B to produce a package of bolts.He earns a profit ₹35 per package of nuts and ₹14 per package of bolts.How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day?
View SolutionA manufacturer produces pend and pencils. It takes 1 hour of work on machine A and 2 hours on machine B to produce a package of pens while it take 2 hours on machine A and 1 hour on machine B to produce a package of pencils . He earn a profit of Rs. 4.00 per package on pens and Rs. 3.00 per package on pencils. How many packages of each should be produce each day so as to maximize his profit, if he operates his machines for at most 12 hours a day ? Formulate the above information mathematically and then solve.
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionA manufacture produceds two types of steel trunks. He has two machines, A and B. The first type of book case requires 3 hours on machine A and 3 hours on machine B for completion whereas the second type required 3 hours on machine A and 2 hours n machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs.30 and Rs.25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make the maximum profit?
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
View Solution
