A point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.
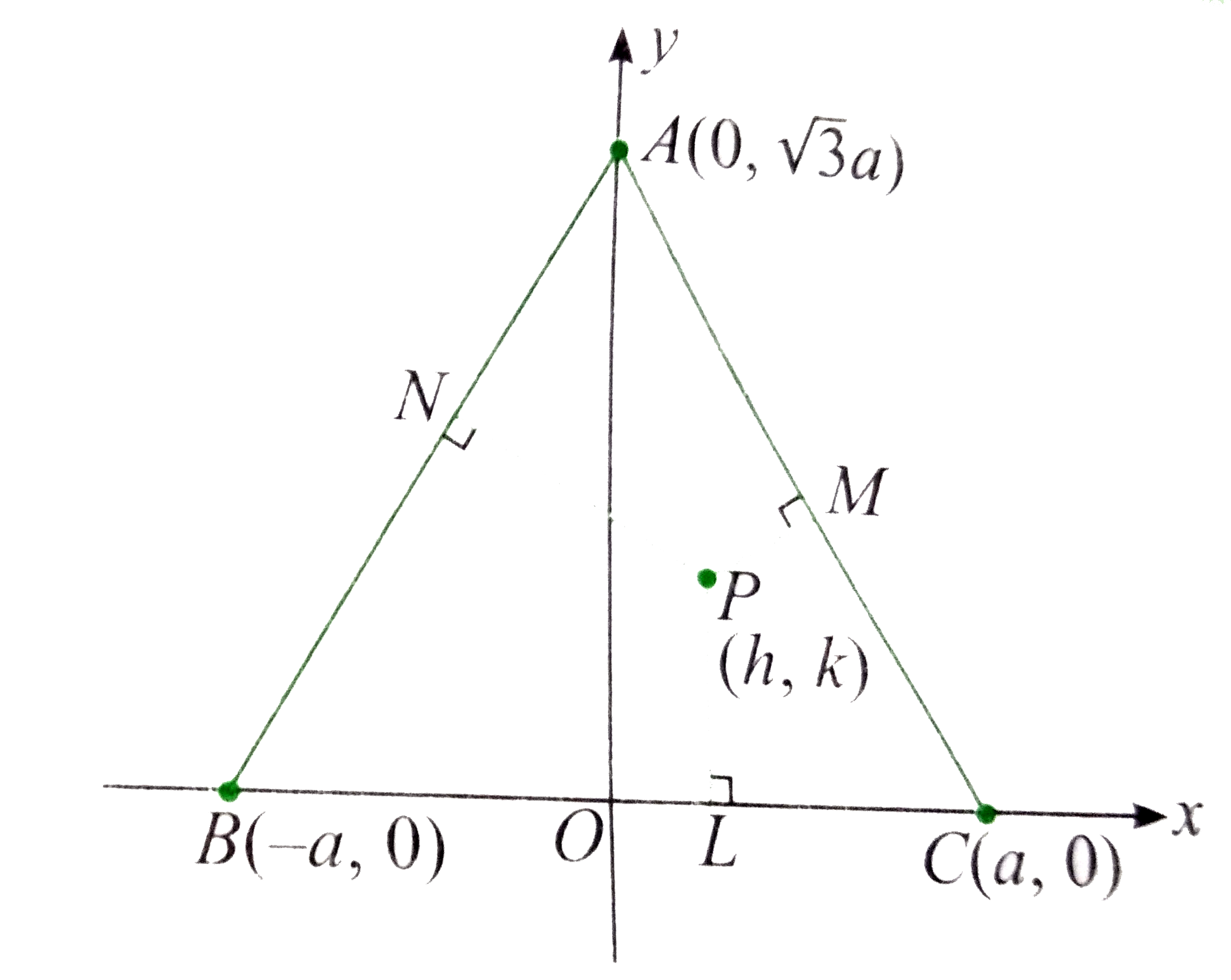
Let vertices B and C of equilateral triangle be (-a,0) and (a,0)
Let point P be (h,k).
Equations of AC and BC are and , respectively.
According to the question,
constant (say
Hence, the required locus is which is a circle
Topper's Solved these Questions
Similar Questions
A point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View Solution
Knowledge Check
The locus of a point which moves such that the sum of the squares of the distances from the three vertices of a triangle is constant, is a circle whose centre is at the:
AIncentre of the triangleBCentroid of the triangleCOrthocentre of the triangleDCircumcentre of the triangleThe locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
AcircleBstraight lineCellipseDnone
A point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point
View SolutionA point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point is
View SolutionThe sum of the perpendiculars drawn from an interior point of an equilateral triangle is 20 cm. What is the length of side of the triangle ?
View SolutionProve that the sum of the squares of the reciprocals of two perpendicular diameter of an ellipse is constant.
View SolutionProve that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View Solution
