A random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
To solve the problem, we will follow these steps:
Step 1: Understand the Probability Distribution
We have the random variable X with the following values and their corresponding probabilities:
- X=1 with probability P(X=1)=k
- X=2 with probability P(X=2)=2k
- X=3 with probability P(X=3)=3k
- X=4 with probability P(X=4)=4k
Step 2: Set Up the Equation for Total Probability
For a valid probability distribution, the sum of all probabilities must equal 1:
P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
Substituting the probabilities, we get:
k+2k+3k+4k=1
Step 3: Simplify the Equation
Combine the terms on the left side:
10k=1
Step 4: Solve for k
Now, solve for k:
k=110
Step 5: Find the Probabilities
Now that we have k, we can find the individual probabilities:
- P(X=1)=k=110
- P(X=2)=2k=210=15
- P(X=3)=3k=310
- P(X=4)=4k=410=25
Step 6: Calculate P(X≥3)
Now, we need to find P(X≥3), which is the sum of the probabilities of X=3 and X=4:
P(X≥3)=P(X=3)+P(X=4)
Substituting the values we found:
P(X≥3)=310+410=710
Final Answer
Thus, the value of P(X≥3) is:
710
We have the random variable X with the following values and their corresponding probabilities:
- X=1 with probability P(X=1)=k
- X=2 with probability P(X=2)=2k
- X=3 with probability P(X=3)=3k
- X=4 with probability P(X=4)=4k
For a valid probability distribution, the sum of all probabilities must equal 1:
P(X=1)+P(X=2)+P(X=3)+P(X=4)=1
Substituting the probabilities, we get:
k+2k+3k+4k=1
Combine the terms on the left side:
10k=1
Now, solve for k:
k=110
Now that we have k, we can find the individual probabilities:
- P(X=1)=k=110
- P(X=2)=2k=210=15
- P(X=3)=3k=310
- P(X=4)=4k=410=25
Now, we need to find P(X≥3), which is the sum of the probabilities of X=3 and X=4:
P(X≥3)=P(X=3)+P(X=4)
Substituting the values we found:
P(X≥3)=310+410=710
Thus, the value of P(X≥3) is:
710
Topper's Solved these Questions
Similar Questions
A random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of k
View SolutionA random variable has the following probability distribution:
X=xi: 0 1 2 3 4 5 6 7
P(X=xi):0 2p 2p 3p p2 2p2 7p2 2p
The value of p is
a. 110
b. −1
c. −110
d. 15
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionA random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
View SolutionIf X is a random variable with probability distribution as given below: X=xi: 0 1 2 3 P(X=xi):k 3k 3k k The value of k and its variance are (A) 18,2227 (B) 18,2327 (C) 18,2427 (D) 18,34
View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View SolutionA random variable X has the following distribution .

The value of k and P(X<4) are equal to
View SolutionA random variable X has the following probability distribution:
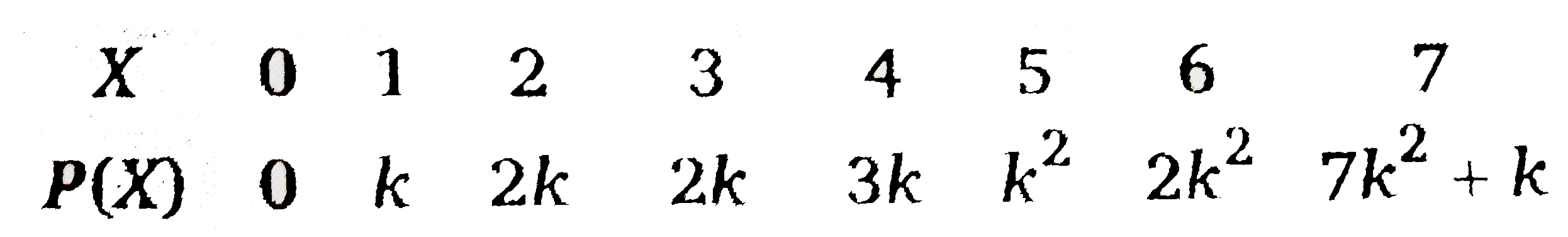
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View Solution
