A tangent to the circle x2+y2=1 through the point (0, 5) cuts the circle x2+y2=4 at P and Q. If the tangents to the circle x2+y2=4 at P and Q meet at R, then the coordinates of R are
(8√6/5,4/5)
(8√6/5),−4/5)
(−8√6/5),−4/5)
none of these
The correct Answer is:A
Clearly, PQ is the chord of contact of tangents drawn from R(α,β) , to the circle x2+y2=4. So, its equation is
αx+βy=4 ...(i)
It passes through (0, 5) . Therefore, β=45
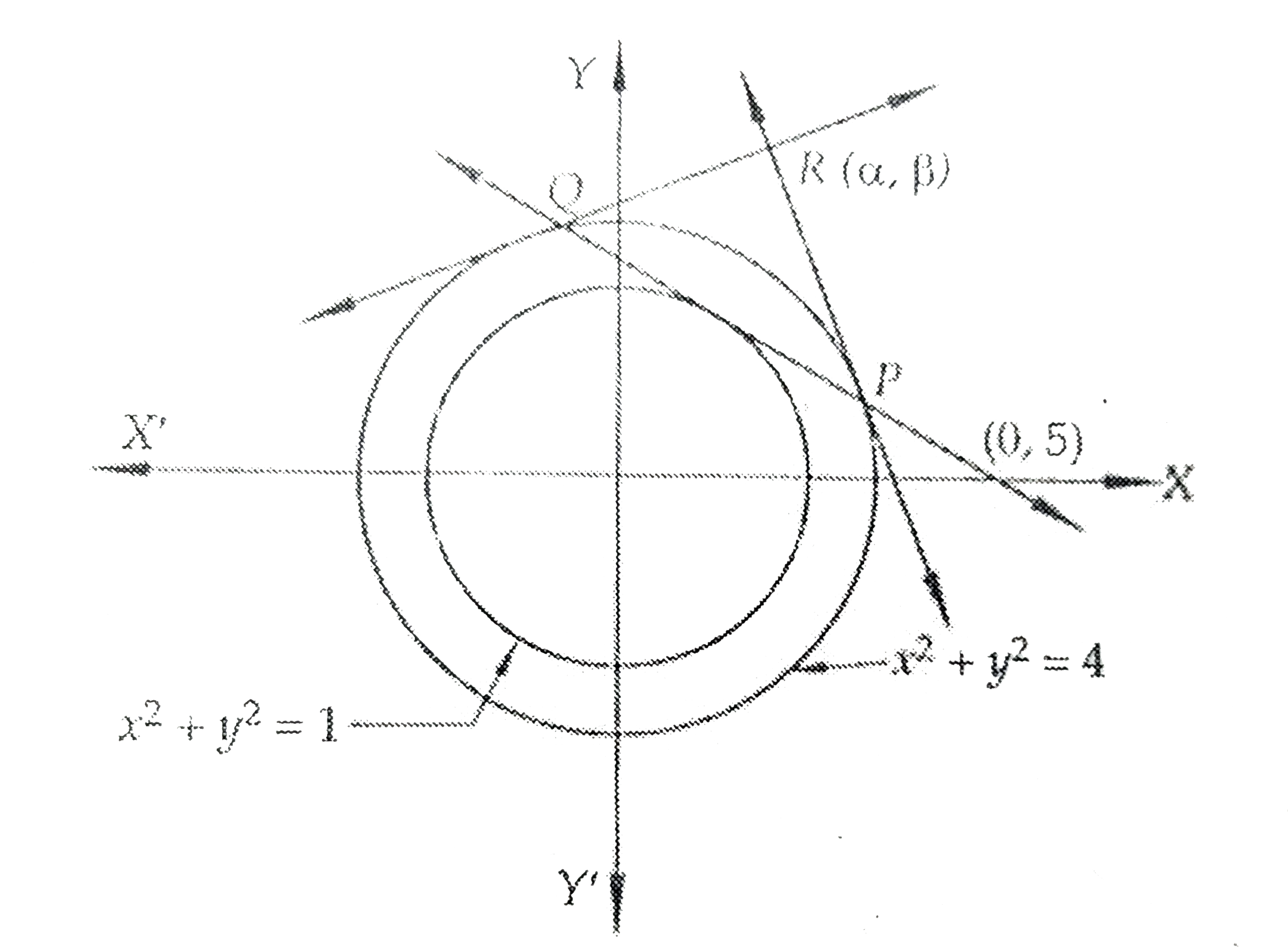
Since PQ touches x2+y2=1.
∴4√α2+β2=1⇒α2+β2=16⇒α2=16−1625⇒α=±8√65
Thus, the coordinates of R the (±8√6/5,4/5)
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the points A(2, 5) and B are symmetrical about the tangent to the circle x2+y2−4x+4y=0 at the origin, then the coordinates of B, are
A(5, -2)B(1, 5)C(5, 2)Dnone of these - Question 2 - Select One
Tangent to the curve y=x2+6 at a point P(1, 7) touches the circle x2+y2+16x+12y+c=0 at a point Q. Then the coordinates of Q are
A(−6,−11)B(−9,−13)C(−10,−15)D(−6,−7) - Question 3 - Select One
Equation of tangent to the circle x2+y2=50 at the point where the line x+7=0 meets the circle
A7x+y=50Bx+7y=50Cx±7y=50D7x±y=50
If tangent at (1,2) to the circle x2+y2=5 intersect the circle x2+y2=9 at A and B and tangents at A and B meets at C. Find the coordinate of C
View SolutionA line passing through the points A(1.−2) cuts the circle x2+y2−y=0 at PandQ. Then the maximum value of |AP−AQ| is
View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
View SolutionIf the tangent from a point p to the circle x2+y2=1 is perpendicular to the tangent from p to the circle x2+y2=3 , then the locus of p is
View SolutionA circle touching the line x+y−2=0 at (1,1) and cuts the circle x2+y2+4x+5y−6=0 at P and Q. Then
View Solution

