Question

A triangle if its perimeter is $10.4cm$ and two angles are ${45}^{\circ }\text{and}{120}^{\circ }$ .

Explanation

Let `ABC` be a triangle. Then, given perimeter = `10.4 cm` i.e., `AB + BC + CA = 10.4cm` and two angles are `45^(@) and 120^(@)` .
say `angleB = 45^(@) and angleC = 120^(@)`
Now, to construct the `Delta ABC` use the following steps.
(i) Draw a line segment say XY and equal to perimeter i.e., `AB + BC + CA = 10.4cm` (ii) Make angle `angleLXY = angleB = 45^(@) and angleMYX = angleC = 120^(@)`.
(iii) Bisect `angleLXY and angleMYX` and let these bisectors intersect at a point A (say).

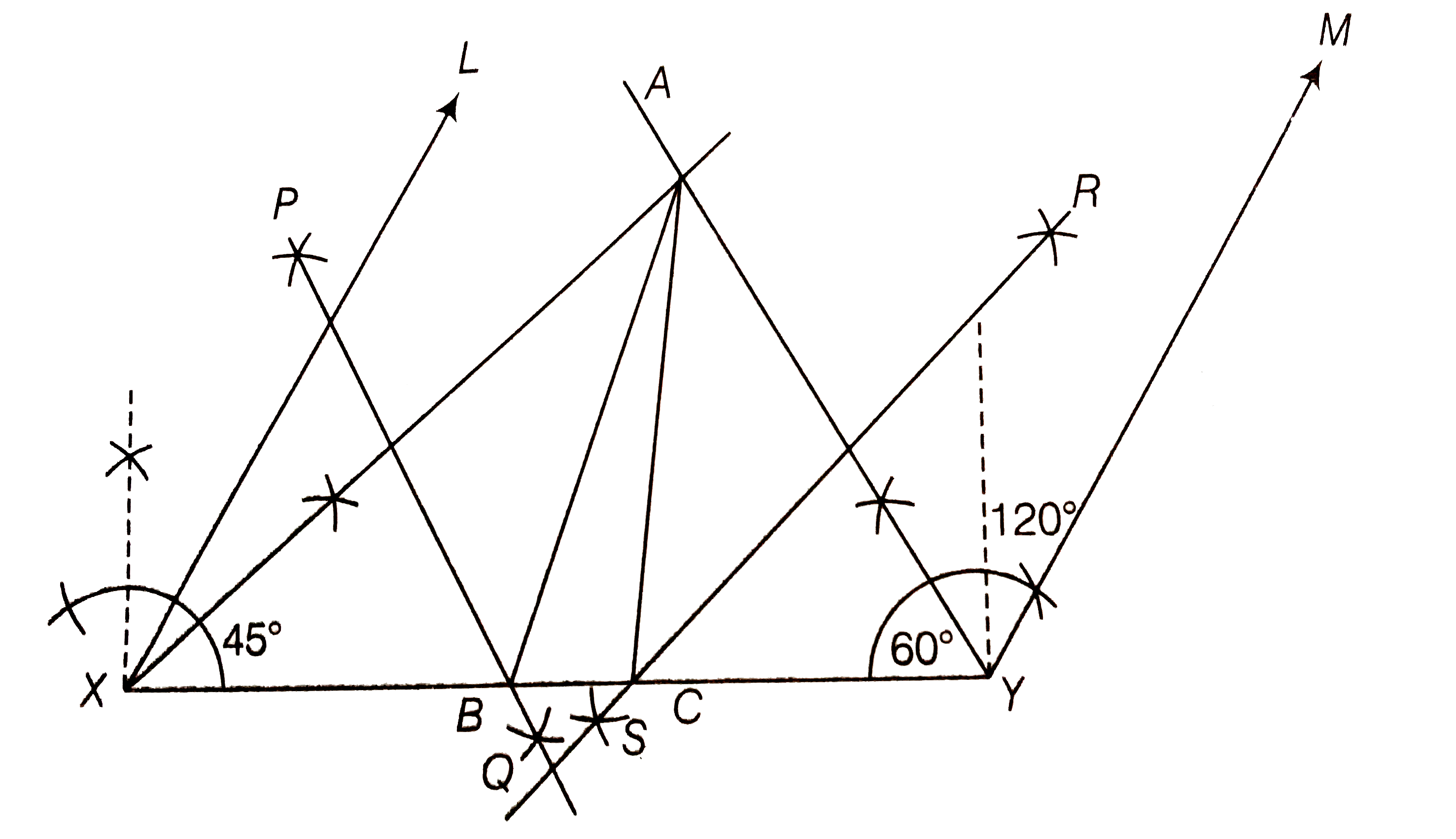
(iv) Draw perpendicular bisectors PQ and RS of AX and AY, respectively.
(v) Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC. Thus , `DeltaABC` is the required triangle.
Justification Since, B lies on the perpendicular bisector PQ of AX.
`:.` XB = AB
Since, C lies on the perpendicular bisector RS of AY.
`:.` CY = AC
Thus, `AB + BC + CA = XB + CY = XY`
Again, `angleBAX = angleAXB` [`because` in `DeltaAXB`, AB = XB]....(i)
Also, `angleABC = angleBAX + angleAXB` [`because angleABC` is an exterior angle of `DeltaAXB`]
= `angle AXB + angleAXB` [from Eq. (i)]
= `2 angleAXB= angleLXY` [`because` AX is a bisector of `angleLXB`]
Also, `angleCAY = angleAYC` [`because in DeltaAYC`, AC = CY]
`:. angleACB = angleCAY + angleAYC` [`because angle ACB` is an exterior angle of `DeltaAYC`]
= `angleCAY + angleCAY`
= `2 angleCAY = angleMYX` [`because` AY is a bisector of `angleMYX`]
Thus, our construction is justified.