are respectively the smallest and longest sides of a quadrilateral
(see Fig. 7.50). Show that and

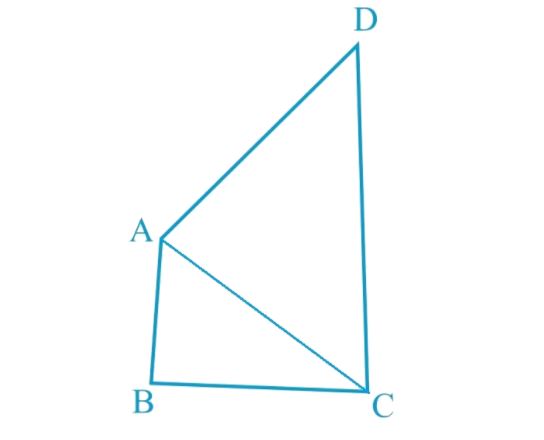
Given: AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD
To prove: ∠A > ∠C and ∠B > ∠D
Let's join vertex A to C as shown below.
In the above ΔABC,
AB < BC (given AB is the smallest side of quadrilateral ABCD)
∠ACB < ∠BAC (Angle opposite to the smaller side is smaller) ... (1)
In ΔADC,
AD < CD (given CD is the largest side of quadrilateral ABCD)
∠ACD < ∠CAD (Angle opposite to the smaller side is smaller) ... (2)
On adding Equations (1) and (2), we obtain
∠ACB + ∠ACD < ∠BAC + ∠CAD
∠C < ∠A
This means, ∠A > ∠C
Hence Proved.
Let's now join BD.
In ΔABD,
AB < AD (Given AB is the smallest side of quadrilateral ABCD)
∠ADB < ∠ABD (Angle opposite to the smaller side is smaller) ...(3)
In ΔBDC,
BC < CD (Given CD is the largest side of quadrilateral ABCD)
∠BDC < ∠CBD (Angle opposite to the smaller side is smaller) ... (4)
On adding equations (3) and (4), we obtain
∠ADB + ∠BDC < ∠ABD + ∠CBD
∠D < ∠B
This means, ∠B > ∠D
Hence, proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.1
8 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERTCHAPTER - TRIANGLESEXERCISE - Solved Examples
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERTCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - EXERCISE 13.8
10 Videos
Similar Questions
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see th e given figure). Show that ∠A>∠C and ∠B>∠D

View SolutionIn Figure, AB and CD are respectively the smalles and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D.

View SolutionAB and CD are respectively the smallest and largest sides of a quadrilateral ABCD. Show that ∠A>∠Cand∠B>∠C.

View SolutionIn Figure, AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D
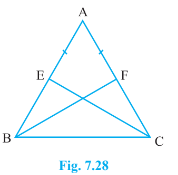
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn quadrilateral ABCD, side DC is largest. Show that AB+AD>DC−BC.
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionThe diagonals of cyclic quadrilateral ABCD are congruent. Show that AD=BC and seg AB || seg CD.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View SolutionA circle touches all the four sides of a quadrilateral ABCD . Prove that: AB+CD=BC+DA .
View Solution
