AB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CP
The correct Answer is:10cm
To solve the problem, we will use the property of intersecting chords in a circle. The property states that if two chords AB and CD intersect at a point P inside the circle, then:
APCP=PDPB
Given:
- AB=24cm
- AP=4cm
- PD=8cm
We need to find CP.
1. Identify the lengths:
- We know AP=4cm and PD=8cm.
- Let CP=xcm.
- To find PB, we can use the total length of chord AB:
PB=AB−AP=24cm−4cm=20cm
2. Set up the proportion:
- Using the property of intersecting chords:
APCP=PDPB
- Substitute the known values:
4x=820
3. Cross-multiply to solve for x:
- Cross-multiplying gives:
4⋅20=8⋅x
- This simplifies to:
80=8x
4. Solve for x:
- Divide both sides by 8:
x=808=10cm
Thus, the length of CP is 10cm.
Final Answer:
CP=10cm
- AB=24cm
- AP=4cm
- PD=8cm
- We know AP=4cm and PD=8cm.
- Let CP=xcm.
- To find PB, we can use the total length of chord AB:
PB=AB−AP=24cm−4cm=20cm
- Using the property of intersecting chords:
APCP=PDPB
- Substitute the known values:
4x=820
- Cross-multiplying gives:
4⋅20=8⋅x
- This simplifies to:
80=8x
- Divide both sides by 8:
x=808=10cm
CP=10cm
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)3videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)8videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)9videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS7videos
BANKING (RECURRING DEPOSIT ACCOUNTS)
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
Similar Questions
AB and CD are two chords of a circle intersecting at a point P inside the circle. If
AP=3cm, PB= 2.5cm and CD= 6.5 cm, determine CP.View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
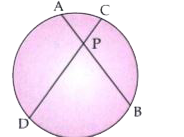 View Solution
View SolutionIn a circle, chords AB and CD intersect at a point R inside the circle. If AR : RB = 1:4 and CR: RD = 4:9, then the ratio AB: CD is
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionAB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
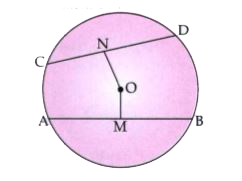 View Solution
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DPView Solution

