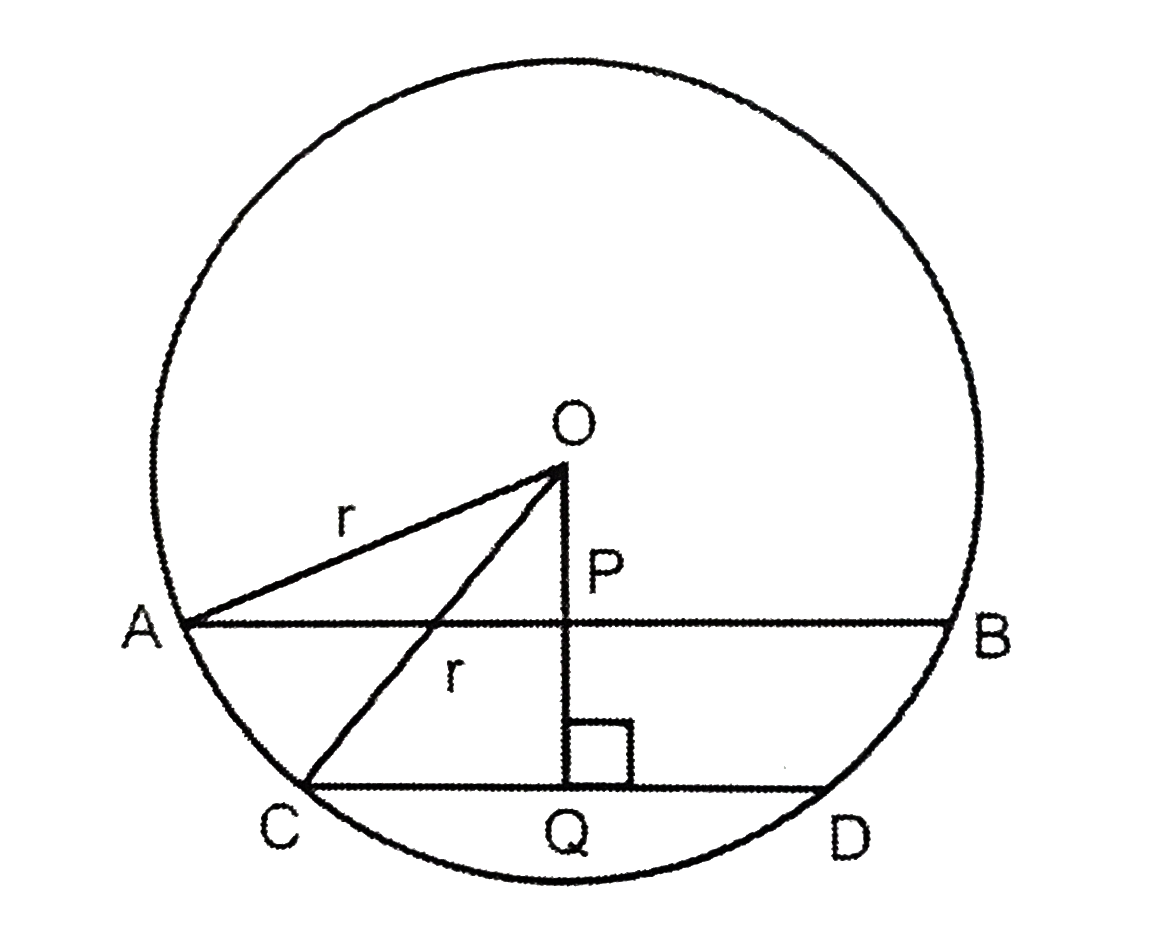
AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
The correct Answer is:r=13cm
To find the radius of the circle given two parallel chords AB and CD, we can follow these steps:
1. Draw the Circle and Chords:
- Draw a circle with center O.
- Draw two parallel chords AB and CD such that AB = 10 cm and CD = 24 cm. Place AB above CD, with a distance of 17 cm between them.
2. Label Distances:
- Let the distance from the center O to chord AB be OP=x.
- The distance from the center O to chord CD will then be OQ=17−x (since the total distance between the two chords is 17 cm).
3. Bisect the Chords:
- Since the perpendicular from the center of the circle to a chord bisects the chord:
- For chord AB, let AP=PB=AB2=102=5 cm.
- For chord CD, let CQ=QD=CD2=242=12 cm.
4. Apply the Pythagorean Theorem:
- For triangle OPB (right triangle):
OB2=OP2+PB2⟹r2=x2+52⟹r2=x2+25(Equation 1)
- For triangle OQD (right triangle):
OD2=OQ2+QD2⟹r2=(17−x)2+122⟹r2=(17−x)2+144(Equation 2)
5. Set Equations Equal:
- Since both expressions equal r2:
x2+25=(17−x)2+144
6. Expand and Simplify:
- Expand (17−x)2:
(17−x)2=289−34x+x2
- Substitute back into the equation:
x2+25=289−34x+x2+144
- Cancel x2 from both sides:
25=433−34x
- Rearranging gives:
34x=433−25⟹34x=408⟹x=40834=12
7. Find the Radius:
- Substitute x=12 back into Equation 1:
r2=122+25=144+25=169⟹r=√169=13 cm
Final Answer:
The radius of the circle is 13 cm.
---
- Draw a circle with center O.
- Draw two parallel chords AB and CD such that AB = 10 cm and CD = 24 cm. Place AB above CD, with a distance of 17 cm between them.
- Let the distance from the center O to chord AB be OP=x.
- The distance from the center O to chord CD will then be OQ=17−x (since the total distance between the two chords is 17 cm).
- Since the perpendicular from the center of the circle to a chord bisects the chord:
- For chord AB, let AP=PB=AB2=102=5 cm.
- For chord CD, let CQ=QD=CD2=242=12 cm.
- For triangle OPB (right triangle):
OB2=OP2+PB2⟹r2=x2+52⟹r2=x2+25(Equation 1)
- For triangle OQD (right triangle):
OD2=OQ2+QD2⟹r2=(17−x)2+122⟹r2=(17−x)2+144(Equation 2)
- Since both expressions equal r2:
x2+25=(17−x)2+144
- Expand (17−x)2:
(17−x)2=289−34x+x2
- Substitute back into the equation:
x2+25=289−34x+x2+144
- Cancel x2 from both sides:
25=433−34x
- Rearranging gives:
34x=433−25⟹34x=408⟹x=40834=12
- Substitute x=12 back into Equation 1:
r2=122+25=144+25=169⟹r=√169=13 cm
The radius of the circle is 13 cm.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (very Short Answer Question)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
AB and CD are two chords such that AB = 10 cm , CD = 24 cm and AB // CD The distance between the chords is 17 cm . Find the radius of the circle.
View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View Solution
Knowledge Check
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
AB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.
View SolutionAB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CP
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View Solution
