AB is a line segment and P is its midpoint. D and E are points on the same side of AP such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
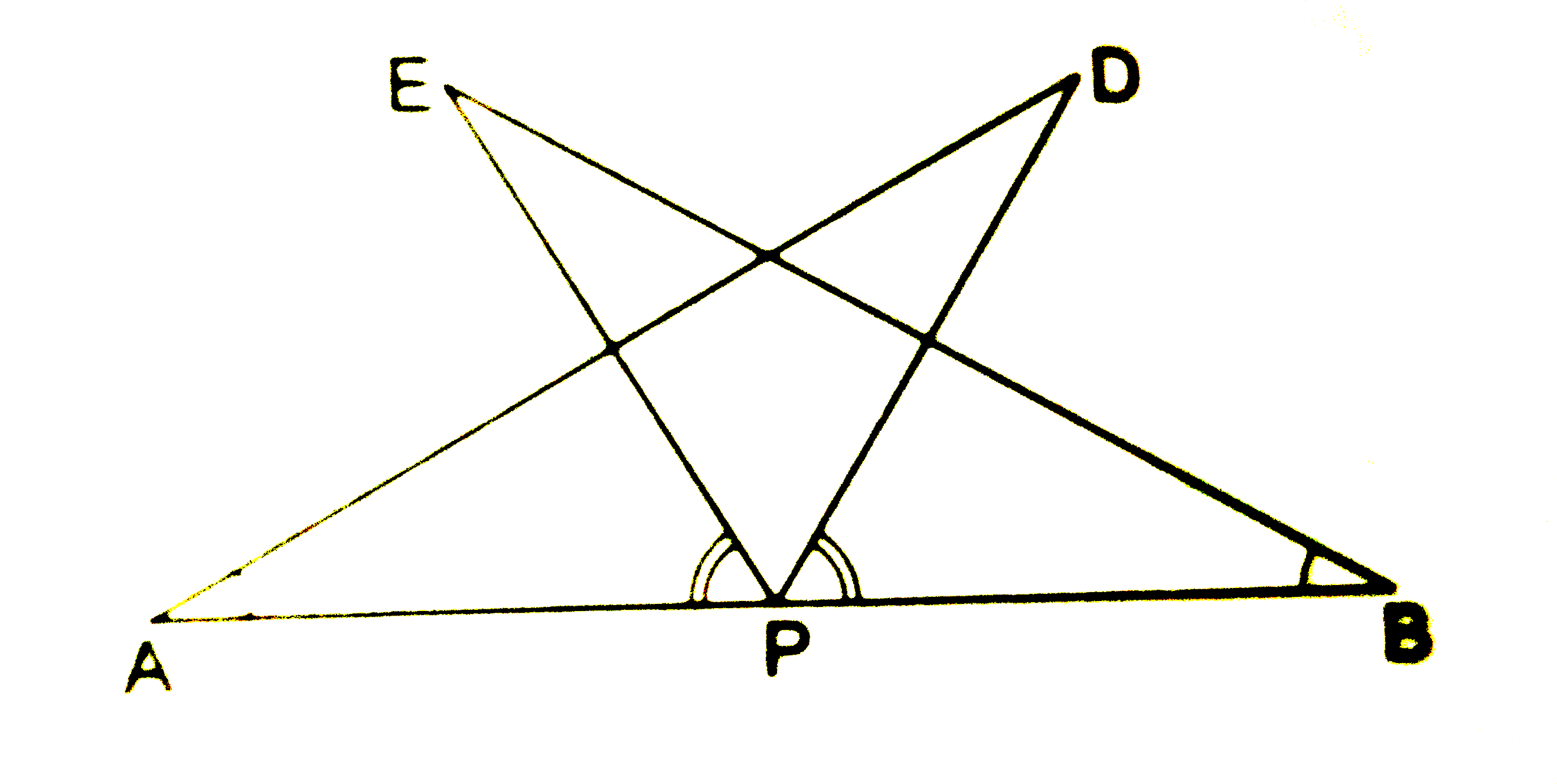
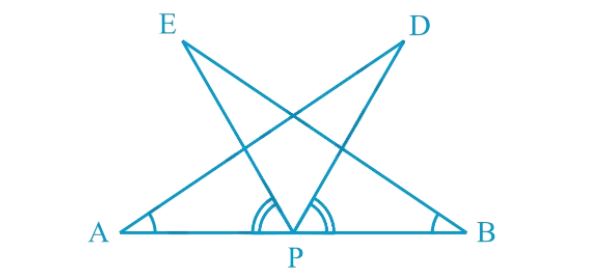
i) It is given that ∠EPA=∠DPB
∠EPA+∠DPE=∠DPB+∠DPE (∠DPE is common)
∴∠DPA=∠EPB
In ΔDAP and ΔEBP,
∠DAP=∠EBP (Given)
AP=BP (P is mid - point of AB)
∠DPA=∠EPB (Proven above)
∴ΔDAP≅ΔEBP(ASA congruence rule)
ii) Since, ΔDAP≅ΔEBP
∴ AD=BE (By CPCT)
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Solved Examples
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.9
3 Videos
Similar Questions
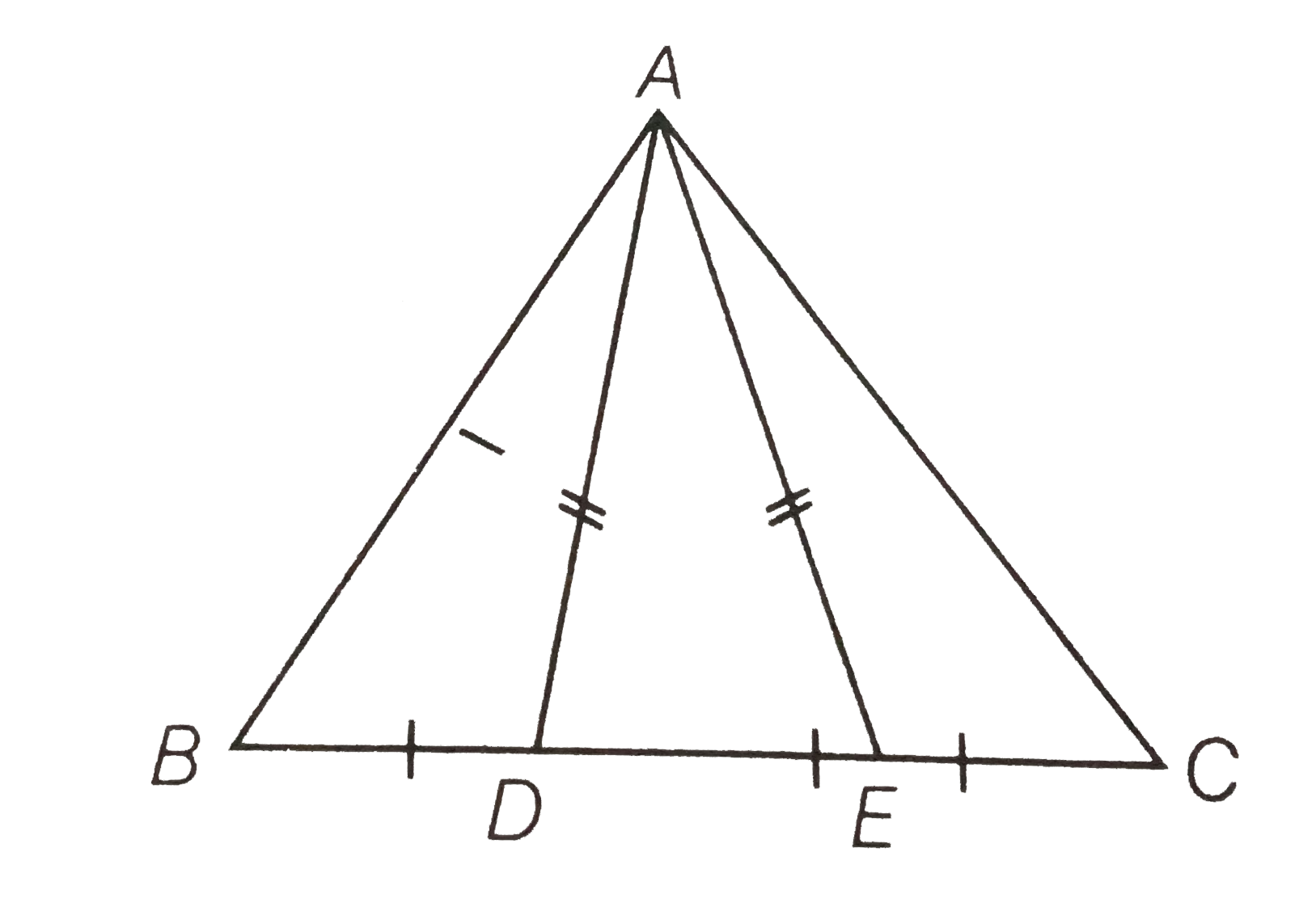
In figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View Solutionif D and E are points on the sides AB and AC of a ΔABC. Such that AB=12 cm, AD=8 cm, AE=12 cm, AC= 18 cm. show that DE||BC.
View SolutionA line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that : QA = QB.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB.
View SolutionAB is a line segment and M is its mid point. Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all thethree semi- circles. Show that AB=6×r
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View Solution
