In quadrilateral ACBD, and AB bisects (see Fig. 7.16). Show that

In
AC=AD
AB=AB
BC=BD.
Similar Questions
In quadrilateral ACBD, AC=AD and AB bisects ∠A . Show that ABC ≅ABD. What can you say about BC and BD?
View SolutionABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
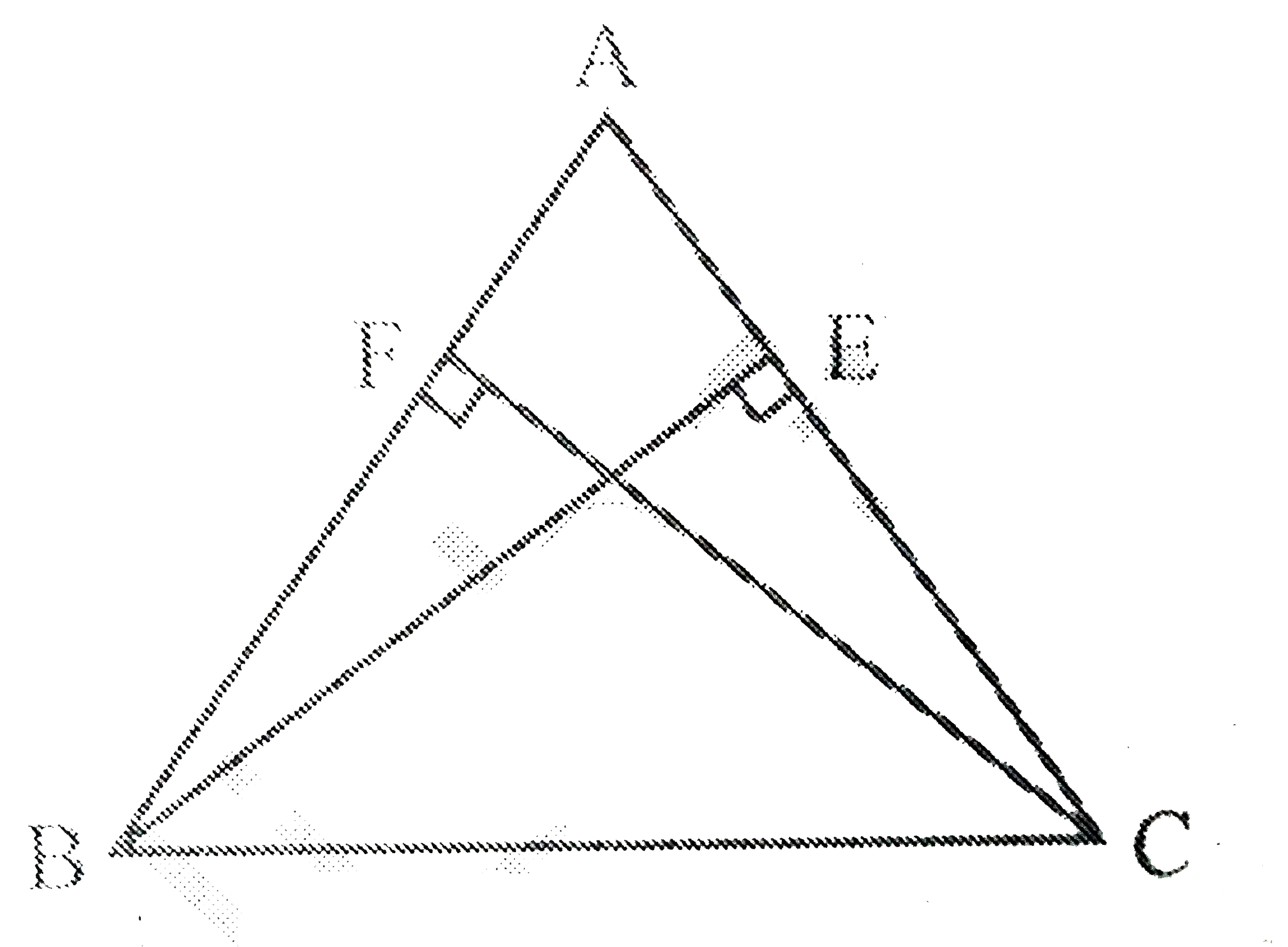
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn a cyclic quadrilateral ABCD , if ∠A=3∠C. Find ∠A
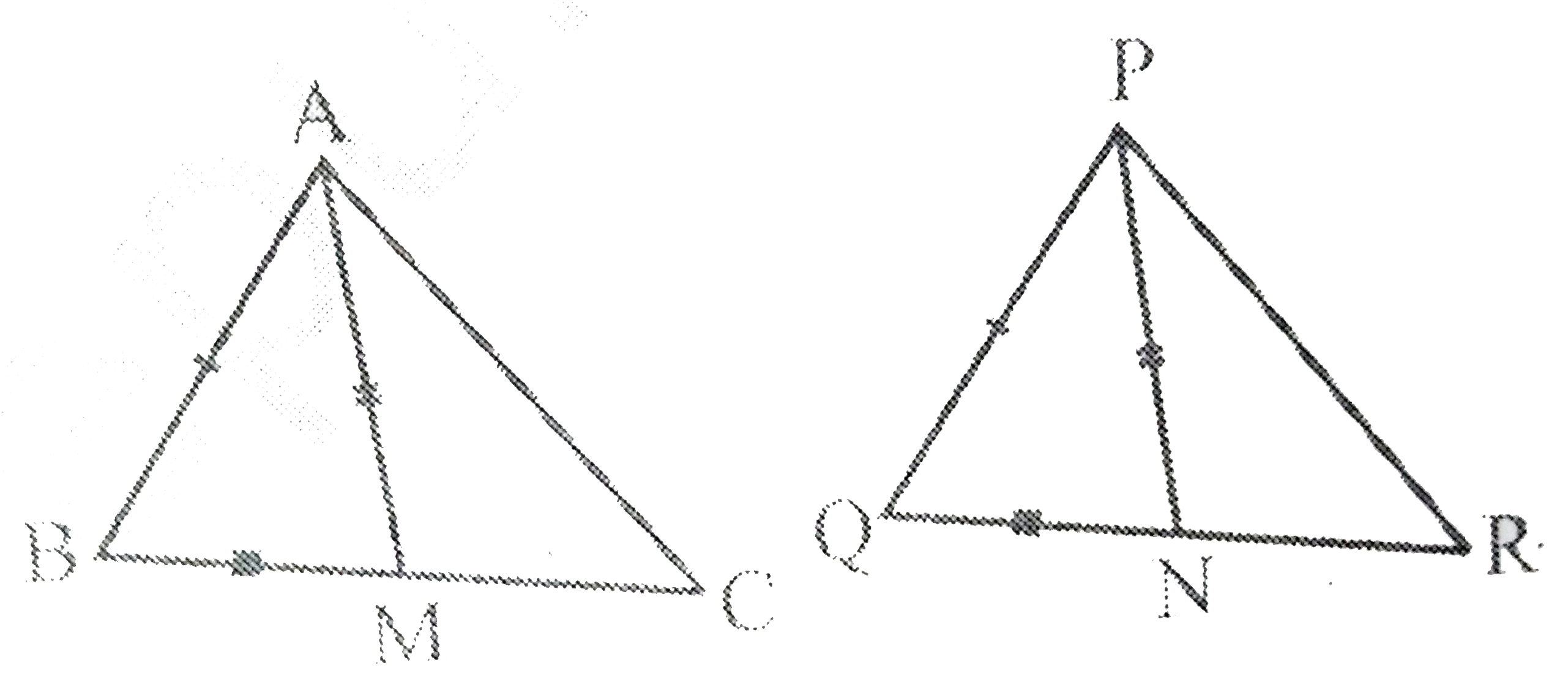
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
View SolutionIn Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
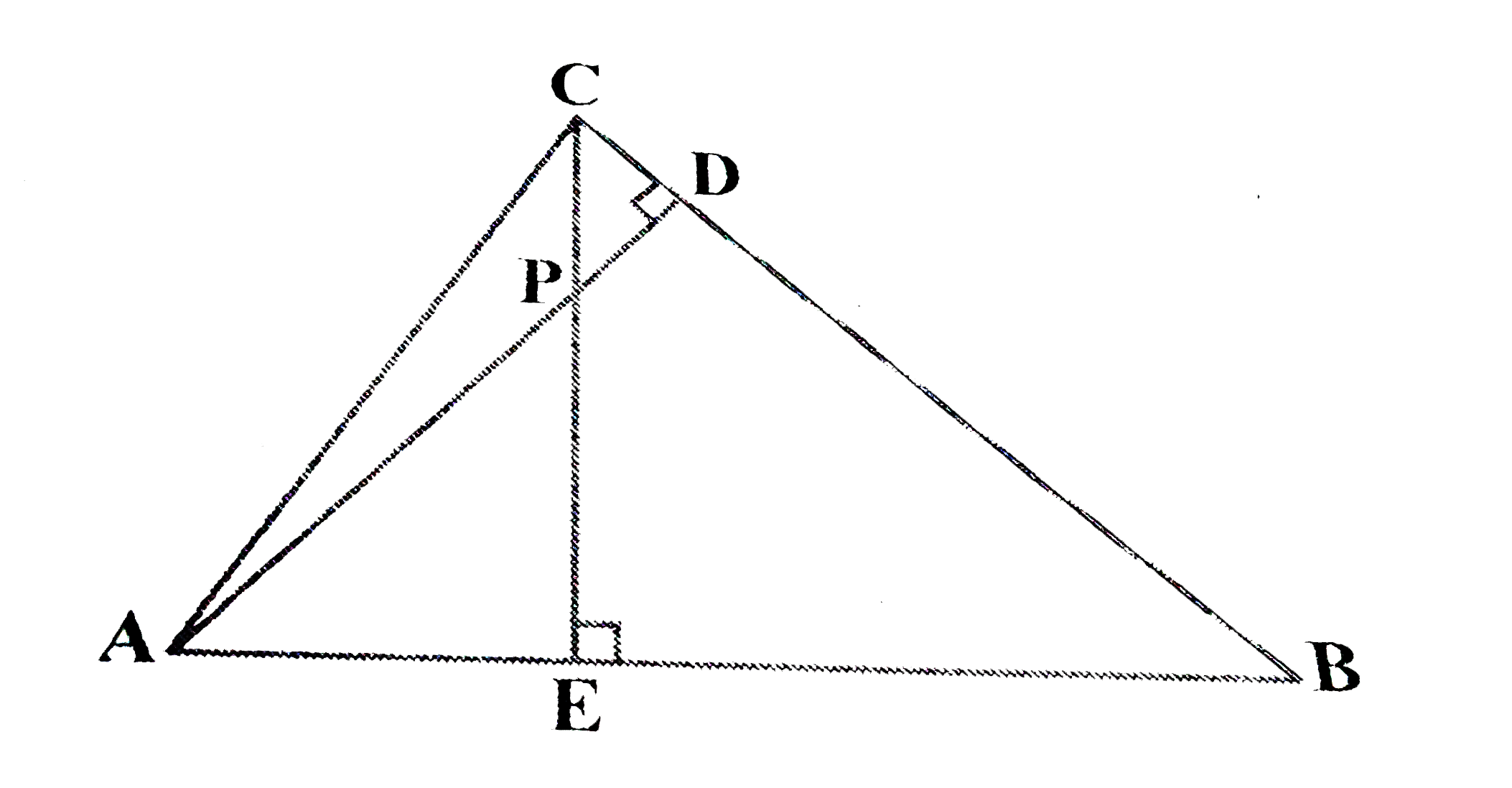
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View Solution