ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that Delta ABE ~= Delta ACF (ii) AB = AC, i.e., ABC is an isosceles triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.35videos
TRIANGLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.46videos
TRIANGLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.5 (Optional)4videos
TRIANGLES
- BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERSICE 13.810videos
SURFACE AREAS AND VOLUMES
Similar Questions
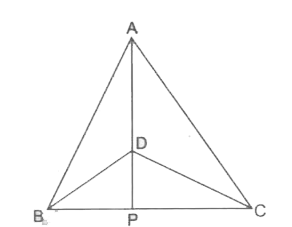
△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) △ABD≅△ACD
(ii) △ABP≅△ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
 04:23View Solution
04:23View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
 03:33View Solution
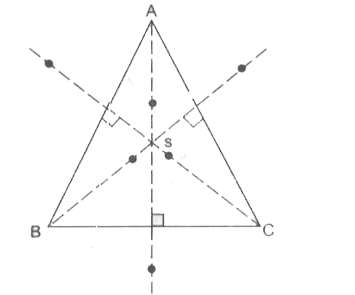
03:33View SolutionABC is a triangle . Locate a point in the interior of △ABC which is equidistant from all the vertices of △ABC.
 14:39View Solution
14:39View SolutionFind the volume of a sphere whose radius is
(i) 7 cm,
(ii) 0.63m03:29View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt03:25View SolutionABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर है। दर्शाइए कि
(i) ΔABE≅ΔACF
(ii) AB=AC, अर्थात ΔABC एक समद्विबाहु त्रिभुज है।
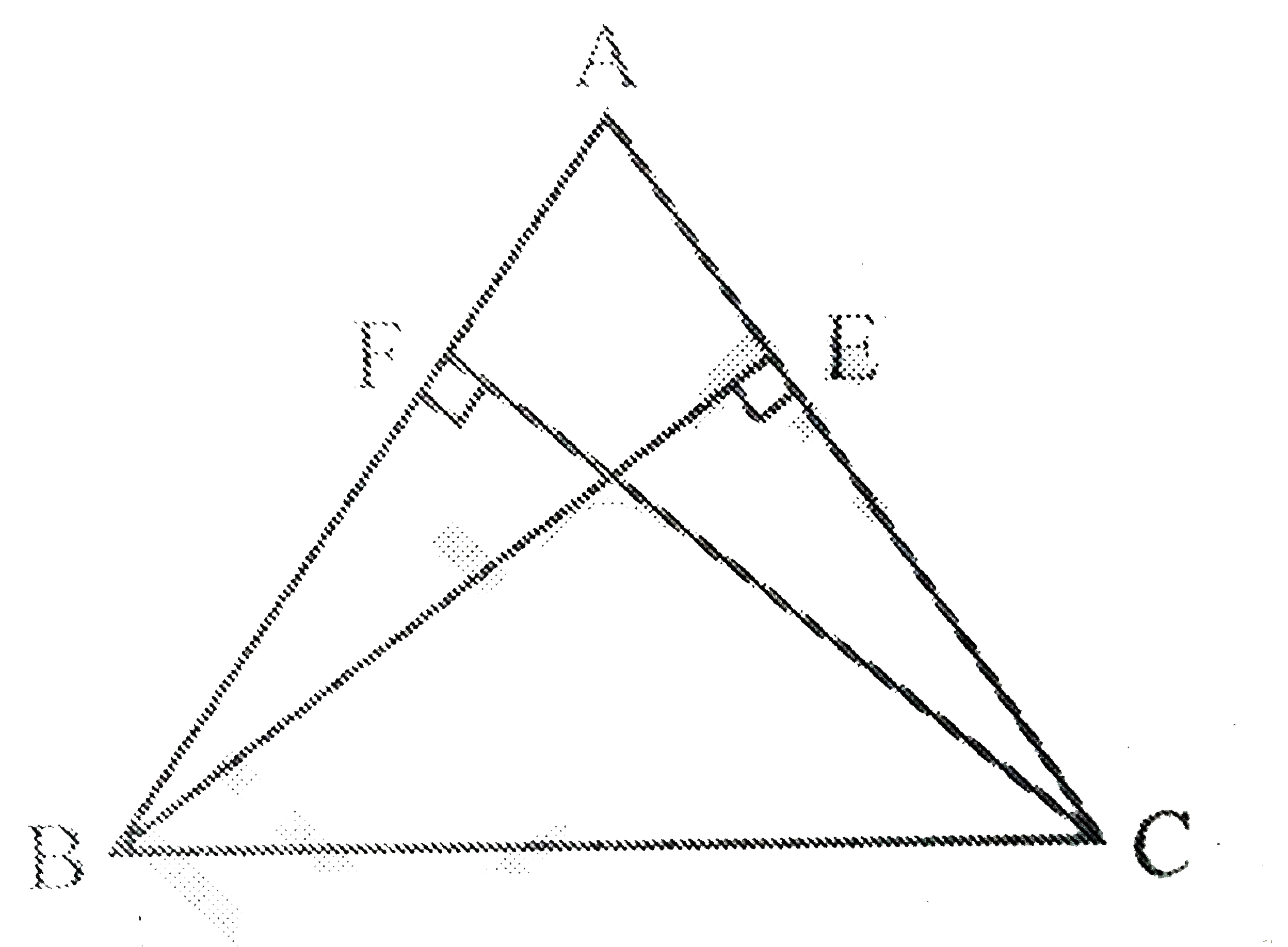 02:34View Solution
02:34View Solutionएक त्रिभुज ABC है जिसमें ऊँचाइयाँ BE और CF भुजाओं AC और AB के बराबर है तो दिखाइये कि-
(i) ΔABE≅ΔACF
(ii) AB=AC,अर्थात ABC एक समद्विबाहु त्रिभुज है ।
 06:57View Solution
06:57View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
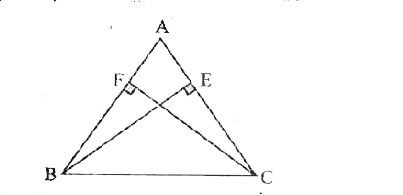 03:06View Solution
03:06View SolutionABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
 05:15View Solution
05:15View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
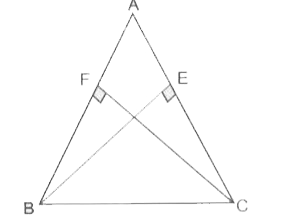 02:48View Solution
02:48View SolutionΔABC లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన AB =AC అనగా ΔABC ఒక సమద్విబహు త్రిభుజామని చూపండి.
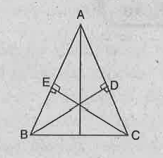 02:47View Solution
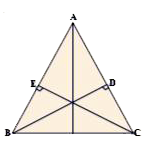
02:47View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
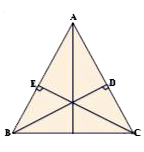 03:39View Solution
03:39View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
 03:49View Solution
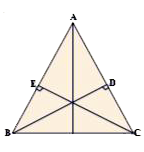
03:49View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
 03:02View Solution
03:02View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i ) △ABE≅△ACF
(ii) AB = AC i.e ABC is an isoceles triangle
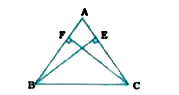 04:05View Solution
04:05View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (See Fig.
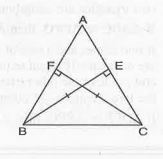 ). Show that these altitudes are equal.04:05View Solution
). Show that these altitudes are equal.04:05View Solution

