ABCD is a cyclic trapezium m, in which AB∣∣DC. If ∠B=75∘ , then find other angles.
To solve the problem step by step, we will use the properties of cyclic quadrilaterals and the fact that angles in parallel lines are supplementary.
1. Identify Given Information:
- We have a cyclic trapezium ABCD where AB is parallel to DC.
- We know that ∠B=75∘.
2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the sum of the opposite angles is 180∘.
- Therefore, we can write:
∠B+∠D=180∘
- Substituting the value of ∠B:
75∘+∠D=180∘
- Solving for ∠D:
∠D=180∘−75∘=105∘
3. Use the Property of Parallel Lines:
- Since AB∥DC, and BC acts as a transversal, we can use the property of co-interior angles:
∠B+∠C=180∘
- Substituting the value of ∠B:
75∘+∠C=180∘
- Solving for ∠C:
∠C=180∘−75∘=105∘
4. Find Angle A Using the Cyclic Property Again:
- Again using the property of cyclic quadrilaterals:
∠A+∠C=180∘
- Substituting the value of ∠C:
∠A+105∘=180∘
- Solving for ∠A:
∠A=180∘−105∘=75∘
5. Summarize the Angles:
- We have found:
- ∠A=75∘
- ∠B=75∘
- ∠C=105∘
- ∠D=105∘
Final Answer:
- ∠A=75∘
- ∠B=75∘
- ∠C=105∘
- ∠D=105∘
- We have a cyclic trapezium ABCD where AB is parallel to DC.
- We know that ∠B=75∘.
- In a cyclic quadrilateral, the sum of the opposite angles is 180∘.
- Therefore, we can write:
∠B+∠D=180∘
- Substituting the value of ∠B:
75∘+∠D=180∘
- Solving for ∠D:
∠D=180∘−75∘=105∘
- Since AB∥DC, and BC acts as a transversal, we can use the property of co-interior angles:
∠B+∠C=180∘
- Substituting the value of ∠B:
75∘+∠C=180∘
- Solving for ∠C:
∠C=180∘−75∘=105∘
- Again using the property of cyclic quadrilaterals:
∠A+∠C=180∘
- Substituting the value of ∠C:
∠A+105∘=180∘
- Solving for ∠A:
∠A=180∘−105∘=75∘
- We have found:
- ∠A=75∘
- ∠B=75∘
- ∠C=105∘
- ∠D=105∘
- ∠A=75∘
- ∠B=75∘
- ∠C=105∘
- ∠D=105∘
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
ABCD is a cyclic trapezium in which, AD| |BC and ∠B=70∘. Find its remaining angles,
View SolutionABCD is a cyclic trapezium with AD∣∣BC. If ∠B=700, determine other three angles of the trapezium.
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionAn angle of a cyclic trapezium is twice the other angle. Find the value of the smaller angle.
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
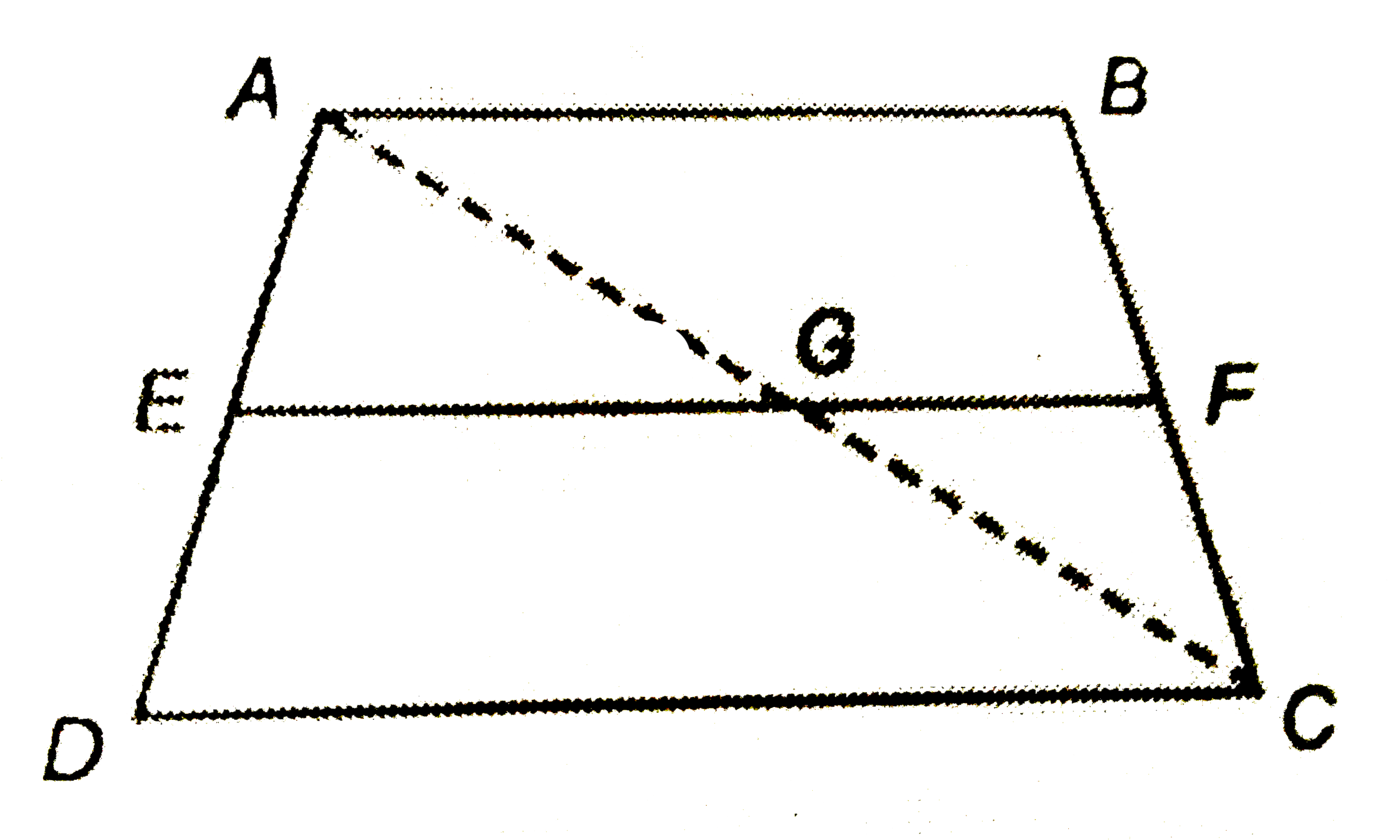
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle ADC=110∘ and angle BAC=50∘. Find angle DAC and angle DCA.
View SolutionIn the given figures ABCD is a trapezium with DC //AB , ∠AOB=126∘and∠DCQ=∠CDP=52∘
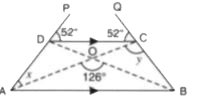
View SolutionABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
View Solution
