ABCD is a parallelogram, G is the point on AB such that AG = 2 GB, E is point on DC such that CE = 2DE and F is the point on BC such that BF = 2FC. Then, match the following:
The correct Answer is:B
We have,
ABCD is a parallelogram,
AG=2 GB, CE =2 DE and
BF = 2 FC.
Let AL be the height of ABCD.
(P) are (ADEG) AG+DE)AL
(Q) Since, AG=2 GB. (given
AB=AG+GB=2GB+GB=3 GB
(R) Since, BF=2 FC
BC=BF+FC=2FC+FC=3FC
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
 View Solution
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
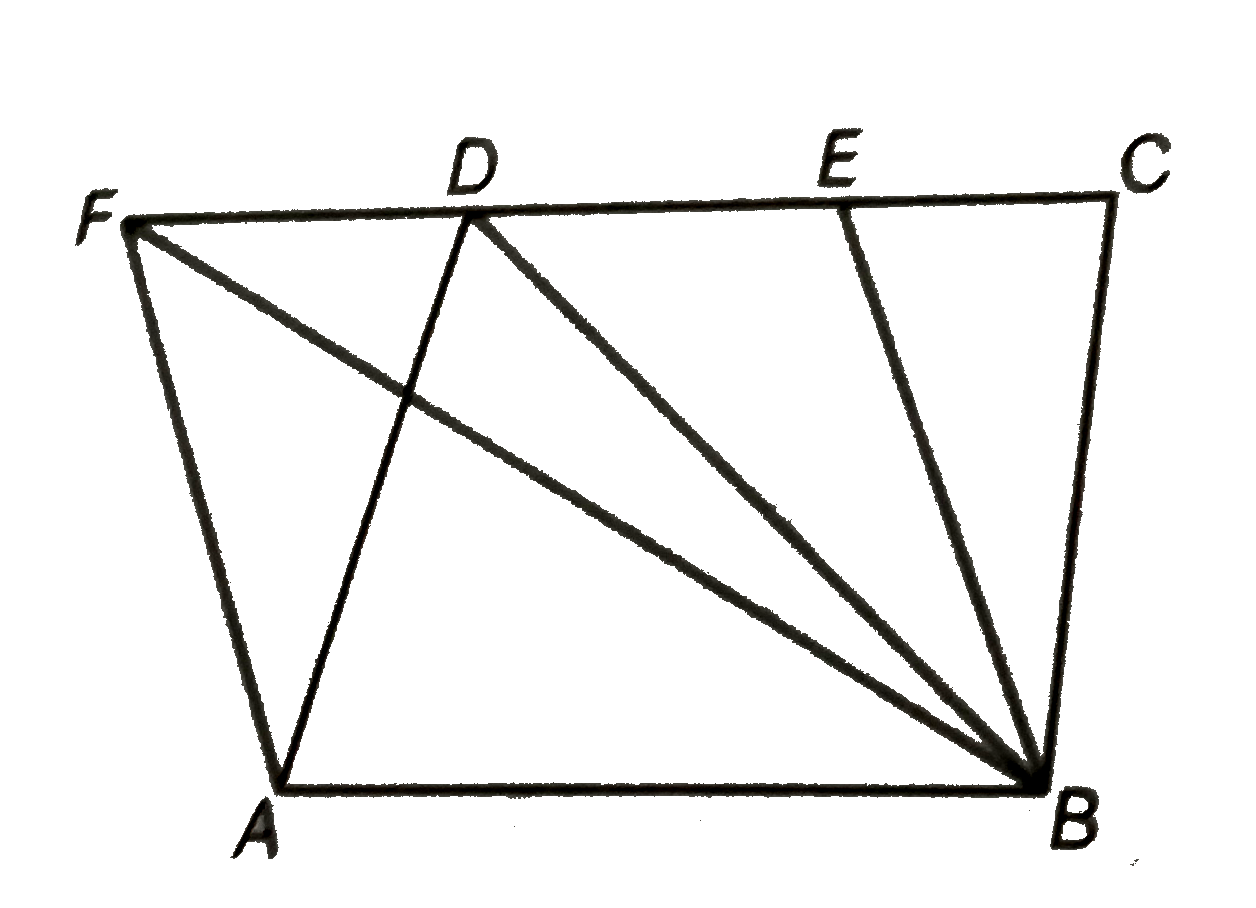
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
 View Solution
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
 View Solution
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).
 View Solution
View Solution

