ABCD is a parallelogram. P is any point on CD. If ar(ΔDPA)=15 cm2 and ar(ΔAPC)=20 cm2, then ar(ΔAPB)=
15 cm2
20 cm2
35 cm2
30 cm2
The correct Answer is:C
To solve the problem, we need to find the area of triangle ΔAPB given that ar(ΔDPA)=15cm2 and ar(ΔAPC)=20cm2.
Step 1: Understand the relationship between the areas of the triangles
In the parallelogram ABCD, we know that triangles DPA and APC share a common base AP and have heights that are perpendicular to this base.
Step 2: Calculate the area of triangle ΔADC
The area of triangle ΔADC can be expressed as the sum of the areas of triangles DPA and APC:
ar(ΔADC)=ar(ΔDPA)+ar(ΔAPC)=15cm2+20cm2=35cm2
Step 3: Use the properties of parallelograms
In a parallelogram, opposite triangles formed by a diagonal have equal areas. Thus, the area of triangle ΔAPB is equal to the area of triangle ΔADC:
ar(ΔAPB)=ar(ΔADC)=35cm2
Final Answer
Therefore, the area of triangle ΔAPB is:
ar(ΔAPB)=35cm2
---
In the parallelogram ABCD, we know that triangles DPA and APC share a common base AP and have heights that are perpendicular to this base.
The area of triangle ΔADC can be expressed as the sum of the areas of triangles DPA and APC:
ar(ΔADC)=ar(ΔDPA)+ar(ΔAPC)=15cm2+20cm2=35cm2
In a parallelogram, opposite triangles formed by a diagonal have equal areas. Thus, the area of triangle ΔAPB is equal to the area of triangle ΔADC:
ar(ΔAPB)=ar(ΔADC)=35cm2
Therefore, the area of triangle ΔAPB is:
ar(ΔAPB)=35cm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
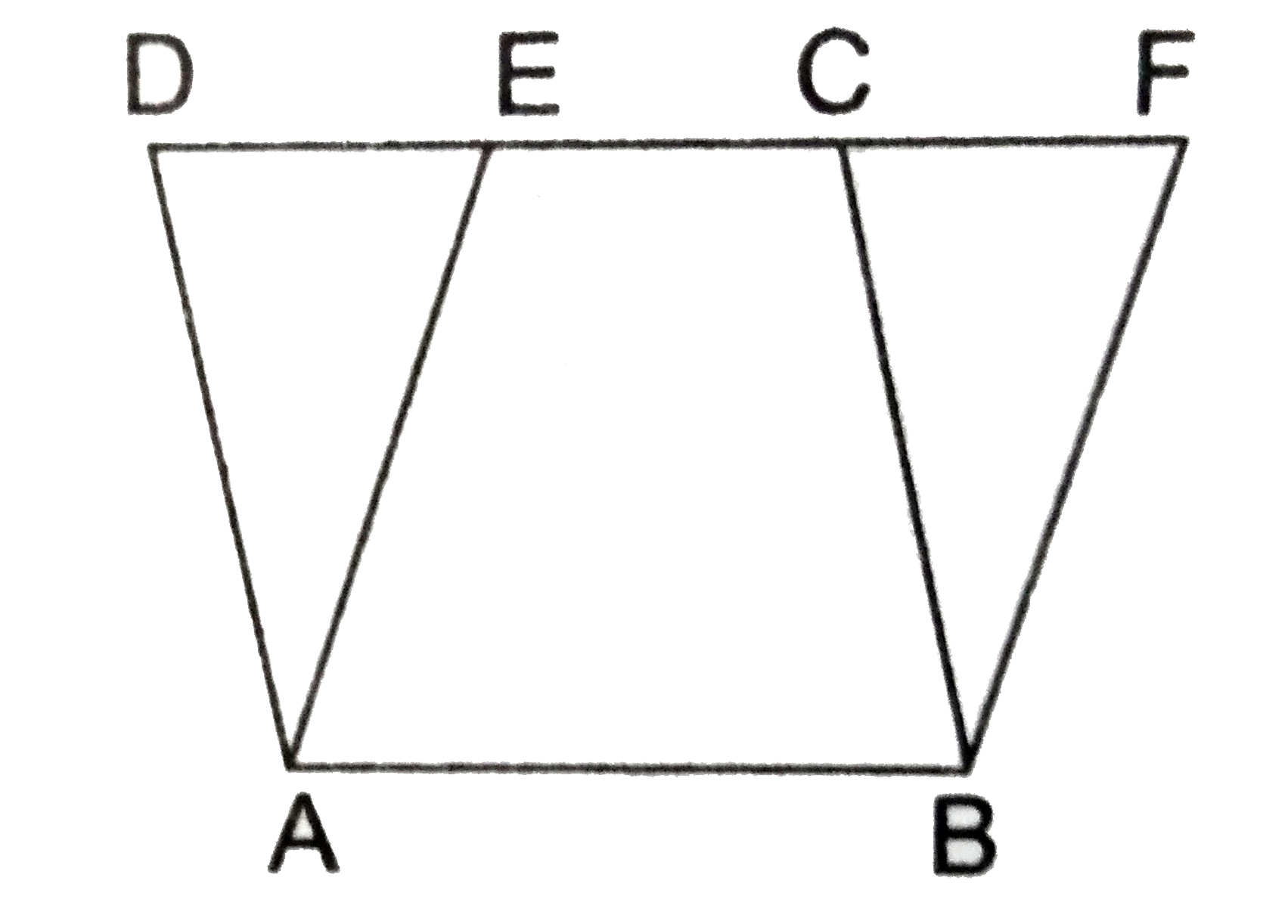 A4cm2B4.8cm2C6cm2D8cm2
A4cm2B4.8cm2C6cm2D8cm2In the given figure, AD is the median and E is any point on AC, such that ar(ΔMDE) : ar(ΔABD) = 2 : 3, then find the ratio of ar(ΔEDC): ar(ΔABC).
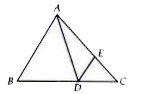 A3 : 4B1 : 6C6 : 1D4 : 3
A3 : 4B1 : 6C6 : 1D4 : 3
In the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View SolutionABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
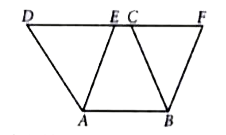
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
View SolutionMNOP is a parallelogram. Q and R are point on sides MN and ON respectively. (△PRM)=12cm2, find ar(△POQ)
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
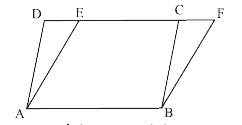
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View Solution