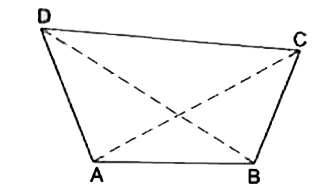
ABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
To determine whether AB+BC+CD+DA>AC+BD for the quadrilateral ABCD, we can use the triangle inequality theorem. Here’s a step-by-step solution:
Step 1: Identify the triangles
We can break down the quadrilateral ABCD into two triangles: △ABC and △ACD.
Step 2: Apply the triangle inequality to triangle ABC
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. For triangle ABC:
AB+BC>AC
This means that the sum of sides AB and BC is greater than the length of side AC.
Step 3: Apply the triangle inequality to triangle ACD
Now, applying the triangle inequality to triangle ACD:
AC+AD>CD
This means that the sum of sides AC and AD is greater than the length of side CD.
Step 4: Combine the inequalities
From the two inequalities we have:
1. AB+BC>AC
2. AD+CD>AC
Now, if we add these two inequalities together:
(AB+BC)+(AD+CD)>AC+AC
This simplifies to:
AB+BC+CD+DA>2AC
Step 5: Apply the triangle inequality to triangle ABD
Next, we can also consider triangle ABD:
AB+AD>BD
Step 6: Apply the triangle inequality to triangle BCD
And for triangle BCD:
BC+CD>BD
Step 7: Combine these inequalities
Adding these inequalities gives:
(AB+AD)+(BC+CD)>BD+BD
This simplifies to:
AB+AD+BC+CD>2BD
Step 8: Conclude the comparison
Now we have two inequalities:
1. AB+BC+CD+DA>2AC
2. AB+BC+CD+DA>2BD
Thus, we can conclude:
AB+BC+CD+DA>AC+BD
Final Answer
Yes, AB+BC+CD+DA>AC+BD.
---
We can break down the quadrilateral ABCD into two triangles: △ABC and △ACD.
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. For triangle ABC:
AB+BC>AC
This means that the sum of sides AB and BC is greater than the length of side AC.
Now, applying the triangle inequality to triangle ACD:
AC+AD>CD
This means that the sum of sides AC and AD is greater than the length of side CD.
From the two inequalities we have:
1. AB+BC>AC
2. AD+CD>AC
(AB+BC)+(AD+CD)>AC+AC
This simplifies to:
AB+BC+CD+DA>2AC
Next, we can also consider triangle ABD:
AB+AD>BD
And for triangle BCD:
BC+CD>BD
Adding these inequalities gives:
(AB+AD)+(BC+CD)>BD+BD
This simplifies to:
AB+AD+BC+CD>2BD
Now we have two inequalities:
1. AB+BC+CD+DA>2AC
2. AB+BC+CD+DA>2BD
AB+BC+CD+DA>AC+BD
Yes, AB+BC+CD+DA>AC+BD.
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.5
8 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.1
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - SOLVED EXAMPLES
6 Videos
- SYMMETRYBOOK - NCERTCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.1
9 Videos
Similar Questions
ABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionShow that in a quandrilateral ABCD,AB+BC+CD+DA<2(BD+AC).
View SolutionABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the area of quadrilateral ABCD ?
View SolutionABCD is a quadrilateral. Forces AB, CB, CD and DA act along its sides. What is their resultant?
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B.
View Solution
