Question

ABCD is a trapezium in which AB||CD and AD = BC. Show that
(i) $\angle A=\angle B\text{and}\angle C=\angle D,\text{(ii)}△ABC\cong △BAD\text{and}$
(ii) AC = BD.

Explanation

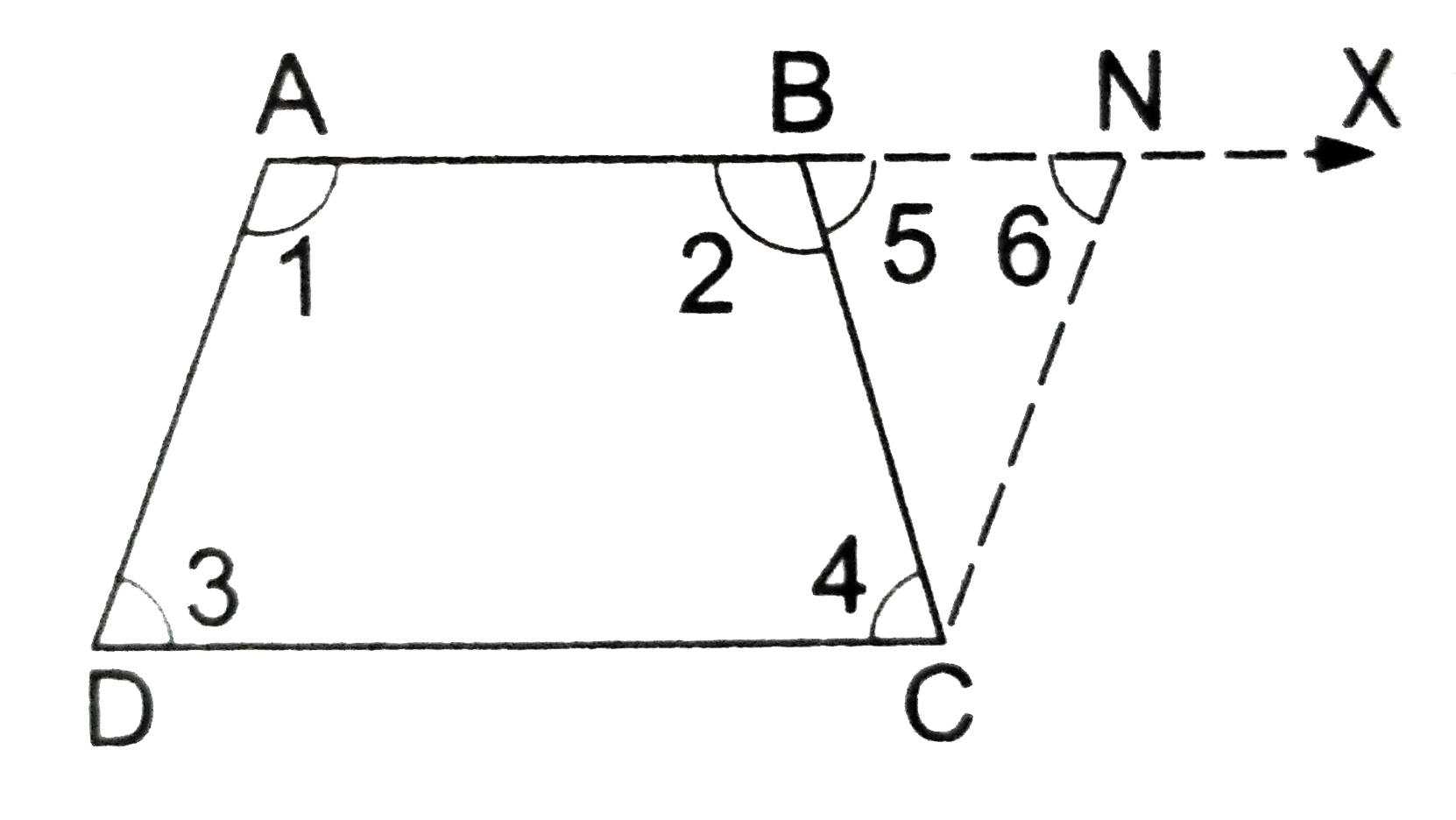
GIVEN A trapezium ABCD in which AB||CD and AD = BC.
TO PROVE (i) `angle A = angle B and angle C = angle D ,`
(ii) ` triangle ABC ~= triangle BAD and`
(ii) AC = BD.
CONSTRUCTION Produce AB to X. Draw CN||DA such that CN meets AX at N.
PROOF We have
AD||NC and AN|| DC (since AB||DC) `rArr` ADCN is a ||gm.
`therefore NC = AD = BC rArr angle 5 = angle 6. " " `...(i)
Now, ` angle 1 + angle 6 = 180^(@) " " ("co-interior " angle )`
`and angle 2 + angle 5 = 180^(@) " " `(linear pair)
`therefore angle 1 = angle 2 " " ` [using (i)].
Now, ` angle 3 = angle 6 " " ("opp. " angle " of a ||gm")`
`therefore angle 3 = angle 4 " " `[using (i)].
Thus, `angle A = angle B and angle C = angle D. `

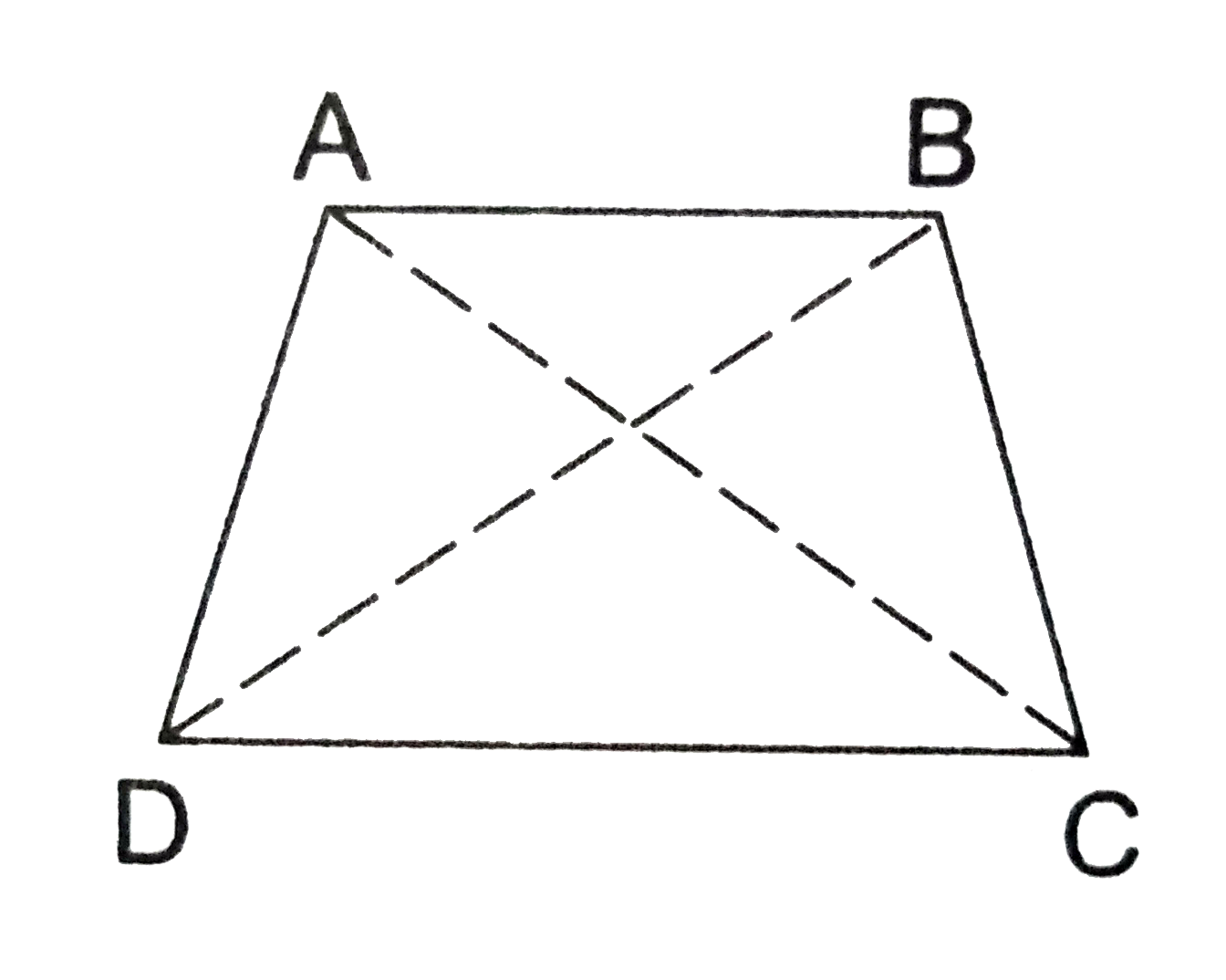
Now, in `triangle ABC and BAD,` we have:
`AB=BA " " ` (common)
`angle ABC = angle BAD " " ("prove that " angle A = angle B)`
`AD = BC " " `(given)
`therefore triangle ABC ~= triangle BAD " " `(SAS-criterion).
And so, `AC = BD " " ` (c.p.c.t.).