ABCD is a trapezium such that AB and CD are parallel and $B C ⊥ C D$ . If $∠ A D B = θ, B C = p and C D = q$ , then AB is equal to

A

$\frac{(p^{2} + q^{2}) sin θ}{p cos θ + q sin θ}$

B

$\frac{p^{2} + q^{2} cos θ}{p cos t h e t + q sin θ}$

C

$\frac{p^{2} + q^{2}}{p^{2} cos θ + q^{2} sin θ}$

D

$\frac{(p^{2} + q^{2}) sin θ}{{(p cos θ + q sin θ)}^{2}}$

Video Solution

Text Solution

Verified by Experts

Let $∠ B D C = α$ . Then, $tan α = \frac{p}{q}$
Clearly, $∠ B D C = ∠ A B D = α$

In $Δ A B D$ , using sine rule, we get
$\frac{A B}{sin θ} = \frac{B D}{sin (π - (θ + α))}$
$\Rightarrow \frac{A B}{sin θ} = (\frac{\sqrt{p^{2} + q^{2}}}{sin (θ + α)} = \frac{\sqrt{p^{2} + q^{2}}}{sin θ cos α + cos θ sin α}$
$\Rightarrow A B = \frac{\sqrt{p^{2} + q^{2}} sin θ}{sin θ (\frac{q}{\sqrt{p^{2} + q^{2}}}) + cos θ (\frac{p}{\sqrt{p^{2} + q^{2}}})}$
$\Rightarrow A B = \frac{(p^{2} + q^{2}) sin θ}{q sin θ + p cos θ}$

|

Updated on:21/07/2023

Class 12 MATHS PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the figure, if $A B = 8, B C = 6, A C = 10 and C D = 9,$ then AD =

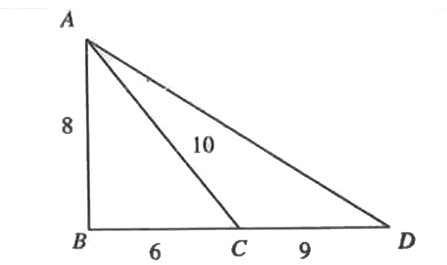A12
B13
C15
D17
Question 2 - Select One

If, in the figure above, CD=1, AB=-2, and AD=6, then BC=
A $5$
B $9$
C $2 + \sqrt{5}$
D $3 \sqrt{5}$

OBJECTIVE RD SHARMA ENGLISH-PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM-Section I - Solved Mcqs

Home
Ask Doubt
Profile