ABCD is a trapezium such that ABandCD are parallel and BC⊥CD. If /_ADB= theta , BC =p and CD=q, then AB is equal to
p2+q2p2cosθ+q2sinθ
(p2+q2)sinθ(pcosθ+qsinθ)2
(p2+q2)sinθpcosθ+qsinθ
p2+q2sinθpcosθ+qsinθ
The correct Answer is:C
To solve the problem, we need to find the length of side AB in trapezium ABCD where AB∥CD and BC⊥CD. Given that ∠ADB=θ, BC=p, and CD=q, we can follow these steps:
1. Identify the trapezium and angles:
- We have trapezium ABCD with AB∥CD and BC⊥CD.
- Given ∠ADB=θ.
2. Label the sides:
- Let BC=p and CD=q.
- Since BC⊥CD, BC acts as a height of the trapezium.
3. Determine angles:
- Let ∠ABD=α. By the properties of parallel lines and transversals, ∠ABD=∠BDC=α.
- Therefore, ∠DAB=180∘−θ−α.
4. Use the right triangle BCD:
- In triangle BCD, we can apply the Pythagorean theorem:
BD2=BC2+CD2=p2+q2
- Thus, BD=√p2+q2.
5. Relate angles using trigonometric ratios:
- From triangle ABD:
tan(α)=BCCD=pq
- Therefore, we can express tan(α) as:
tan(α)=pq
6. Apply the sine rule in triangle ABD:
- According to the sine rule:
ABsin(θ)=BDsin(180∘−θ−α)
- Since sin(180∘−x)=sin(x):
ABsin(θ)=BDsin(θ+α)
7. Substituting BD:
- We know BD=√p2+q2:
AB=√p2+q2⋅sin(θ)sin(θ+α)
8. Using the sine addition formula:
- The sine addition formula gives us:
sin(θ+α)=sin(θ)cos(α)+cos(θ)sin(α)
- Substituting this into our equation for AB:
AB=√p2+q2⋅sin(θ)sin(θ)cos(α)+cos(θ)sin(α)
9. Finding cos(α) and sin(α):
- From triangle BCD:
- cos(α)=q√p2+q2
- sin(α)=p√p2+q2
10. Final expression for AB:
- Substituting cos(α) and sin(α) back into the equation for AB:
AB=√p2+q2⋅sin(θ)sin(θ)⋅q√p2+q2+cos(θ)⋅p√p2+q2
- Simplifying gives:
AB=(p2+q2)sin(θ)qsin(θ)+pcos(θ)
Final Answer:
AB=(p2+q2)sin(θ)qsin(θ)+pcos(θ)
- We have trapezium ABCD with AB∥CD and BC⊥CD.
- Given ∠ADB=θ.
- Let BC=p and CD=q.
- Since BC⊥CD, BC acts as a height of the trapezium.
- Let ∠ABD=α. By the properties of parallel lines and transversals, ∠ABD=∠BDC=α.
- Therefore, ∠DAB=180∘−θ−α.
- In triangle BCD, we can apply the Pythagorean theorem:
BD2=BC2+CD2=p2+q2
- Thus, BD=√p2+q2.
- From triangle ABD:
tan(α)=BCCD=pq
- Therefore, we can express tan(α) as:
tan(α)=pq
- According to the sine rule:
ABsin(θ)=BDsin(180∘−θ−α)
- Since sin(180∘−x)=sin(x):
ABsin(θ)=BDsin(θ+α)
- We know BD=√p2+q2:
AB=√p2+q2⋅sin(θ)sin(θ+α)
- The sine addition formula gives us:
sin(θ+α)=sin(θ)cos(α)+cos(θ)sin(α)
- Substituting this into our equation for AB:
AB=√p2+q2⋅sin(θ)sin(θ)cos(α)+cos(θ)sin(α)
- From triangle BCD:
- cos(α)=q√p2+q2
- sin(α)=p√p2+q2
- Substituting cos(α) and sin(α) back into the equation for AB:
AB=√p2+q2⋅sin(θ)sin(θ)⋅q√p2+q2+cos(θ)⋅p√p2+q2
- Simplifying gives:
AB=(p2+q2)sin(θ)qsin(θ)+pcos(θ)
AB=(p2+q2)sin(θ)qsin(θ)+pcos(θ)
Topper's Solved these Questions
- Solutions of Triangle & Binomial TheoremBook:ALLENChapter:Solutions of Triangle & Binomial TheoremExercise:EXERCISE (O-1)
Explore 11 Videos
- Solutions of Triangle & Binomial TheoremBook:ALLENChapter:Solutions of Triangle & Binomial TheoremExercise:EXERCISE (O-2)
Explore 6 Videos
- Solutions of Triangle & Binomial TheoremBook:ALLENChapter:Solutions of Triangle & Binomial TheoremExercise:EXERCISE-I
Explore 28 Videos
- SOLUTION AND PROPERTIES OF TRIANGLEBook:ALLENChapter:SOLUTION AND PROPERTIES OF TRIANGLEExercise:All Questions
Explore 106 Videos
- TRIGNOMETRIC RATIOS AND IDENTITIESBook:ALLENChapter:TRIGNOMETRIC RATIOS AND IDENTITIESExercise:All Questions
Explore 1 Video
Similar Questions
Knowledge Check
In the figure, if AB=8,BC=6,AC=10andCD=9, then AD =
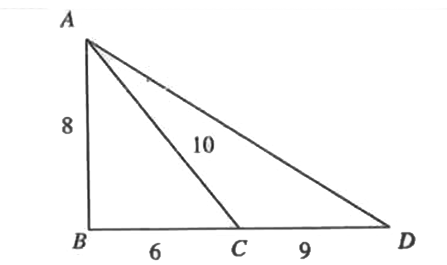 A12B13C15D17
A12B13C15D17
If, in the figure above, CD=1, AB=-2, and AD=6, then BC=A5B9C2+√5D3√5
Let ABCD be a trapezium ,in which AB is parallel to CD, AB =11 ,BC=4,CD=6 and DA=3. the distance between AB and CD is
View SolutionIf a,b,c,d are in H.P., then ab+bc+cd is equal to
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View Solution
