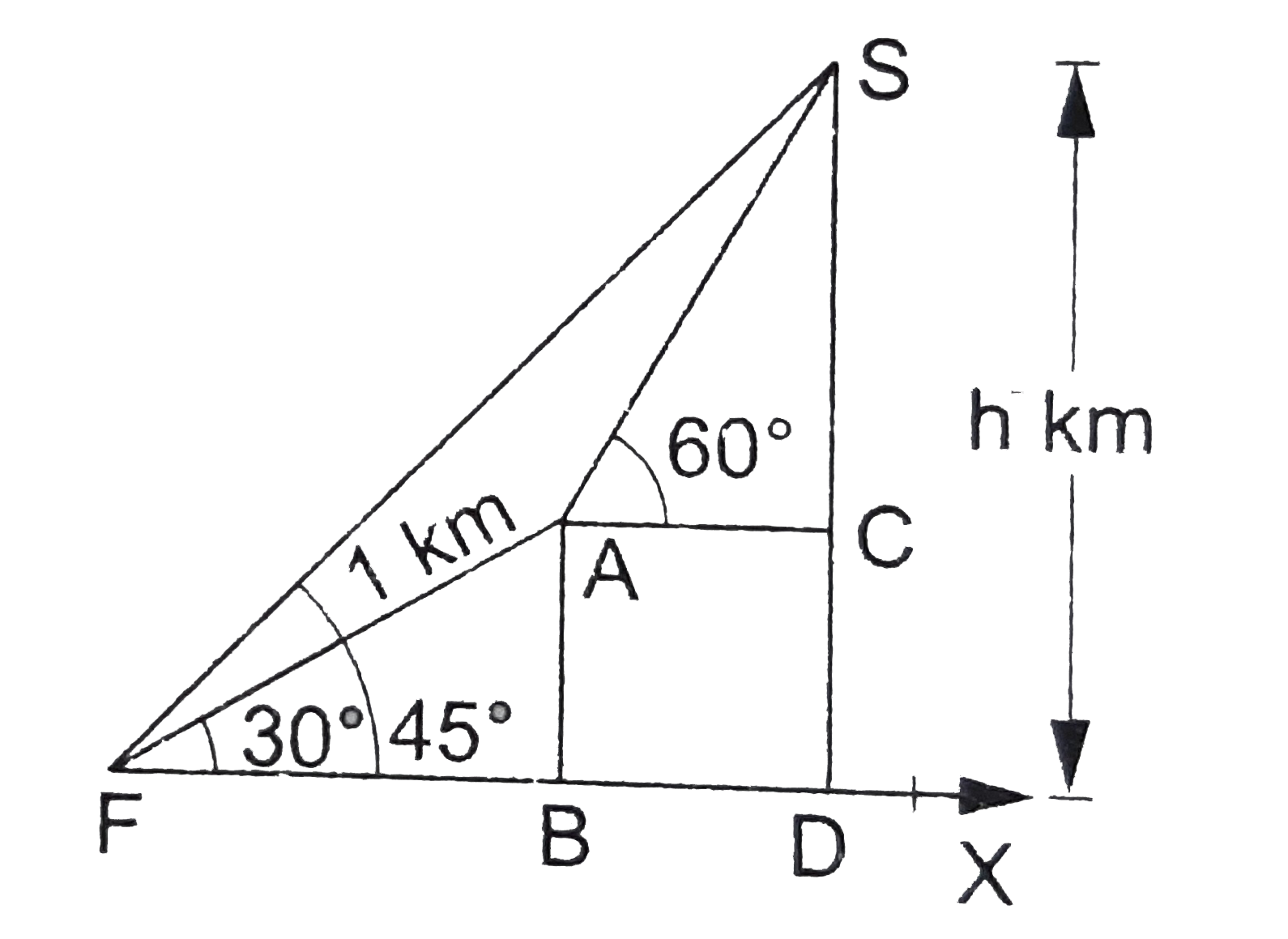
At the foot of a mountain the elevation of its summit is 45∘, after ascending 1000m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ Find the height of the mountain.
Let {F} be the foot and {S} be the summit of the mountain F O S
.
Then, angle O F S=45∘ and therefore∠OSF=45∘.
O F=O S=h {km} (say)
Let F P=1000 {m}=1 {km} be the slope so that
angle O F P=30∘. Draw PM perp O S and PL perp O F.
Join PS. It is given that angle {MPS}=60∘.
In Delta {FPL}, We have
sin30∘=PLPF
Topper's Solved these Questions
Similar Questions
At the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 45∘. After ascending 600 meter towards the mountain, upon an incline of 30∘, the elevation changes to 60∘. Find the height of the mountain.
View Solution
Knowledge Check
At the foot of the mountain, the elevation of its summit is 45∘ , after ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ . The height of the mountain is
A√3+12mB√3−12mC√3+12√3Dnone of theseAt the foot of the mountain the elevation of its summit is 45∘, after ascending 100 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. The height of the mountain is
A√3+12mB√3−13 mC√3+12√3 mDnone of theseAt the foot of a mountain the elevation of its summit is 45∘. After ascending 2000 meter towards the mountain upon an incline of 30∘, the elevation changes to 60∘. What is the height of the mountain.
A2000(√3−1) meterB1000(√3−1) meterC2000(√3+1) meterD1000(√3+1) meter
At the foot of a mountain the elevation of it's peak is found to be(π4) ,after ascending 'h' meters toward the mountain up a slope of π6 inclination,the elevation is found to be π3 .Height of the mountain is
View SolutionAt the foot of a mountain, the angle of elevation of its summit is 45∘. After ascending 1 km towards the mountain up an incline of 30∘, the elevatioon changes to 60∘ (as shown in the given figure). Find the height of the mountain. [Given: √3=1.73.]
View SolutionThe angle of elevation of a tower at a point is 45∘. After going 40 m towards the foot of the tower, the angle of elevation of the tower becomes 60∘. Find the height of the tower.
View SolutionAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
View SolutionFrom a point on the ground, the angle of elevation of a summit is found to be 45∘. After walking 150mt towards the mountain, the angle of elevation of the summit is found to be 60∘. The height of the mountain is:
View Solution
