CD and GH are respectively the bisectors of ∠ACBand ∠EGFsuch that D and H lie on sides AB and FE of ΔABC and ΔEFGrespectively. IfΔABCΔFEG, show that:
(i) CDGH=AGFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
In △ABC and △FEG,
△ABC∼FEG<br>∴/_ACB=/_EGF<br>(Correspond∈g∠sofsimilar△s)<br>Since,DCandGHarebisec→rsof/_ACBand/_EGHrespectively.<br>∴/_ACB=2/_ACD=2/_BCD<br>And/_EGF=2/_FGH=2/_HGE<br>∴/_ACD=/_FGHand/_DCB=/_HGE...................(1)<br>Also/_A=/_Fand/_B=/_E...............(2)<br>In△ACDand△FGH,<br>/_A=/_F(From2)<br>/_ACD=/_FGH(From1)<br>∴By∀criterionofsimilarity△ACD∼△FGH<br>△DCA∼△HGF[(i)and(iii)proved]<br>∴(CD)/(GH)=(AC)/(FG)<br>(Correspond∈gSsofSimilarTri∠s)<br>In△DCBand△HGE,<br>/_B=/_E(From2)<br>/_DCB=/_HGE (From 1)
∴ By AA criterion of similarity △DCB ∼△HGE [(ii) proved]
Topper's Solved these Questions
Similar Questions
CD and GH are respectively the bisectors of ∠ACBand ∠EGFsuch that D and H lie on sides AB and FE of ΔABC and ΔEFGrespectively. IfΔABCΔFEG, show that:
(i) CDGH=AGFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGFView SolutionIn Fig. 4.103, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (FIGURE) ADC~FHG (ii) CDGH=ABFE (iii) CDB~GHE
View SolutionIn Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
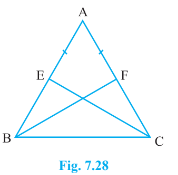
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
 View Solution
View Solution
Identify A, B, C, D, E, F,GView SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.
 View Solution
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.
 View Solution
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View Solution

