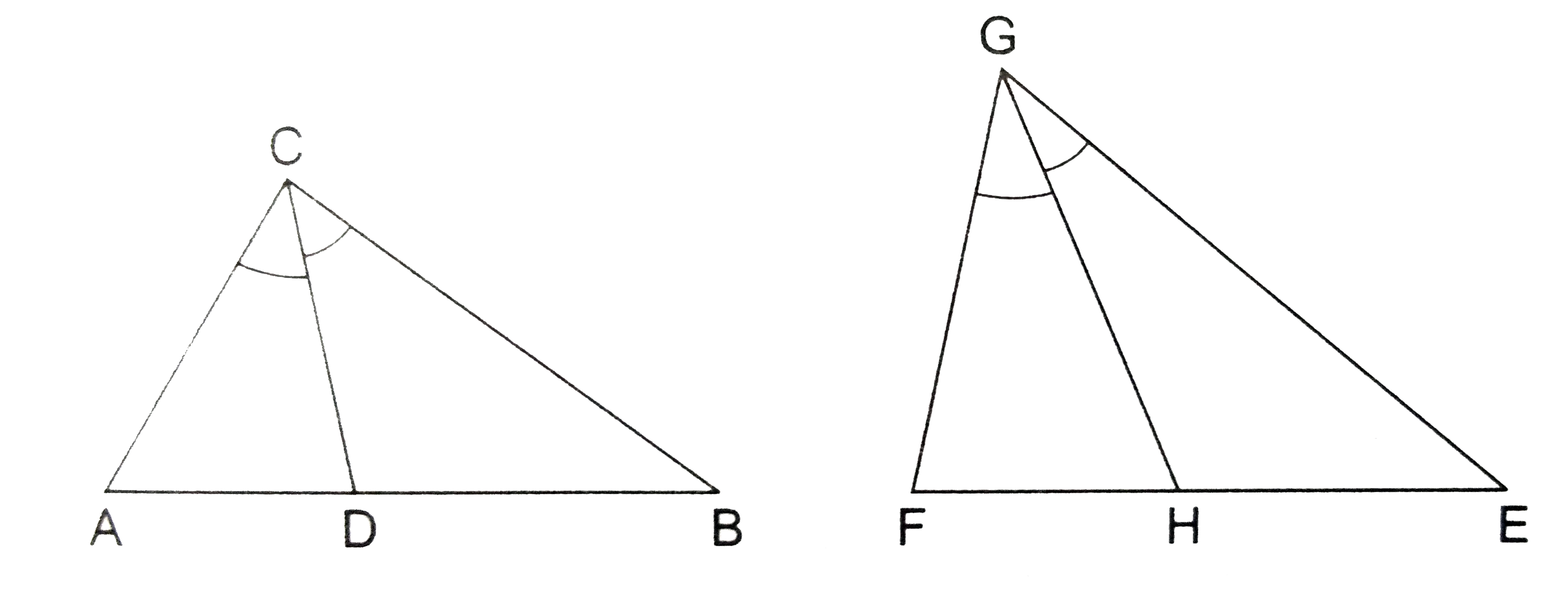
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
CDGH=ACFG
To solve the problem, we need to show that CDGH=ACFG given that triangles ABC and FEG are similar.
1. Identify Given Information:
- We have two triangles, ΔABC and ΔFEG.
- CD is the angle bisector of ∠ACB.
- GH is the angle bisector of ∠EGF.
- The triangles are similar: ΔABC∼ΔFEG.
Hint: Write down all the given information clearly to understand the relationships between the angles and sides.
2. Use Properties of Similar Triangles:
- Since ΔABC∼ΔFEG, the corresponding angles are equal. Thus, we have:
∠A=∠F,∠B=∠E,∠C=∠G
Hint: Remember that in similar triangles, corresponding angles are equal.
3. Apply the Angle Bisector Theorem:
- The angle bisector CD divides ∠ACB into two equal parts:
∠ACD=∠BCD=12∠ACB
- Similarly, the angle bisector GH divides ∠EGF:
∠EGH=∠FGH=12∠EGF
Hint: Use the property of angle bisectors to express the angles in terms of the original angles.
4. Establish Relationships Between Angles:
- From the similarity of triangles, we know:
\angle ACD = \angle EGH \quad \text{(because \angle C = \angle G )}
Hint: Relate the angles formed by the angle bisectors to the corresponding angles of the similar triangles.
5. Use AA Similarity Criterion:
- Since ∠ACD=∠EGH and ∠A=∠F, we can conclude that:
△ACD∼△FGH(by AA criterion)
Hint: Remember that if two angles of one triangle are equal to two angles of another triangle, the triangles are similar.
6. Write the Proportionality of Corresponding Sides:
- From the similarity of triangles, we have:
CDGH=ACFG
Hint: Use the property that corresponding sides of similar triangles are in proportion.
7. Conclusion:
- We have shown that:
CDGH=ACFG
- This completes the proof.
- We have two triangles, ΔABC and ΔFEG.
- CD is the angle bisector of ∠ACB.
- GH is the angle bisector of ∠EGF.
- The triangles are similar: ΔABC∼ΔFEG.
- Since ΔABC∼ΔFEG, the corresponding angles are equal. Thus, we have:
∠A=∠F,∠B=∠E,∠C=∠G
- The angle bisector CD divides ∠ACB into two equal parts:
∠ACD=∠BCD=12∠ACB
- Similarly, the angle bisector GH divides ∠EGF:
∠EGH=∠FGH=12∠EGF
- From the similarity of triangles, we know:
\angle ACD = \angle EGH \quad \text{(because \angle C = \angle G )}
- Since ∠ACD=∠EGH and ∠A=∠F, we can conclude that:
△ACD∼△FGH(by AA criterion)
- From the similarity of triangles, we have:
CDGH=ACFG
- We have shown that:
CDGH=ACFG
- This completes the proof.
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.4 )
9 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.5 )
23 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.2 )
12 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACBand ∠EGFsuch that D and H lie on sides AB and FE of ΔABC and ΔEFGrespectively. IfΔABCΔFEG, show that:
(i) CDGH=AGFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View Solution
Knowledge Check
In which of the following options ,DE ||AB where D and E lie on the sides AC and BC of ΔABC respectively ?
AAD = 6 , EC = 14 , BC = 18 , DC = 21BBE = 20 , Dc = 10 , AC = 25 , BC =36CAC = 10 , Dc = 4 , EC =2 , BC =6DNone of theseThe mid points of AB and AC of the ΔABC are P and Q respectively. If PQ=6cm, then the side BC is
A10 cm.B12 cm.C8 cm.D14 cm.Mid-points of the sides AB and AC of a ΔABC are (3, 5) and (-3, -3) respectively, then the length of the side BC is
A10 unitB20 unitC15 unitD30 unit
CD and GH are respectively the bisectors of ∠ACB and ∠EGFof ΔABC and ΔEFG respectively. If ΔABC~ΔFEG show that :
ΔDCA~ΔHGF
View SolutionIn the given figure, CD and GH are respectively the bisectors of ∠ACBand∠FGEofΔABCandΔEFG respectively . If ΔABC~ΔFEG, prove that :
(a) ΔADC~ΔFHG (b)ΔBCD~ΔEGH (c)CDGH=ACFG
View SolutionIn the given figure, the sides AB and AC of ΔABC have been extended to D and E respectively. If x>y, show that AB>AC.

View SolutionA line cuts two sides AB and AC of ΔABC at points P and Q respectively. Prove A(ΔAPQ)A(ΔABC)=AP×AQAB×AC.
View SolutionIf D and E are the mid points of AB and AC respectively of ΔABC, then the ratio of the areas of ADE and BCED is?
View Solution
