Consider a triangle PQR in which the relation QR2+PR2=5PQ2 holds. Let G be the point of intersection of medians PM and QN. Then ∠QGM is always
less than 45∘
obtuse
a right angle
acute and larger than 45∘
The correct Answer is:C
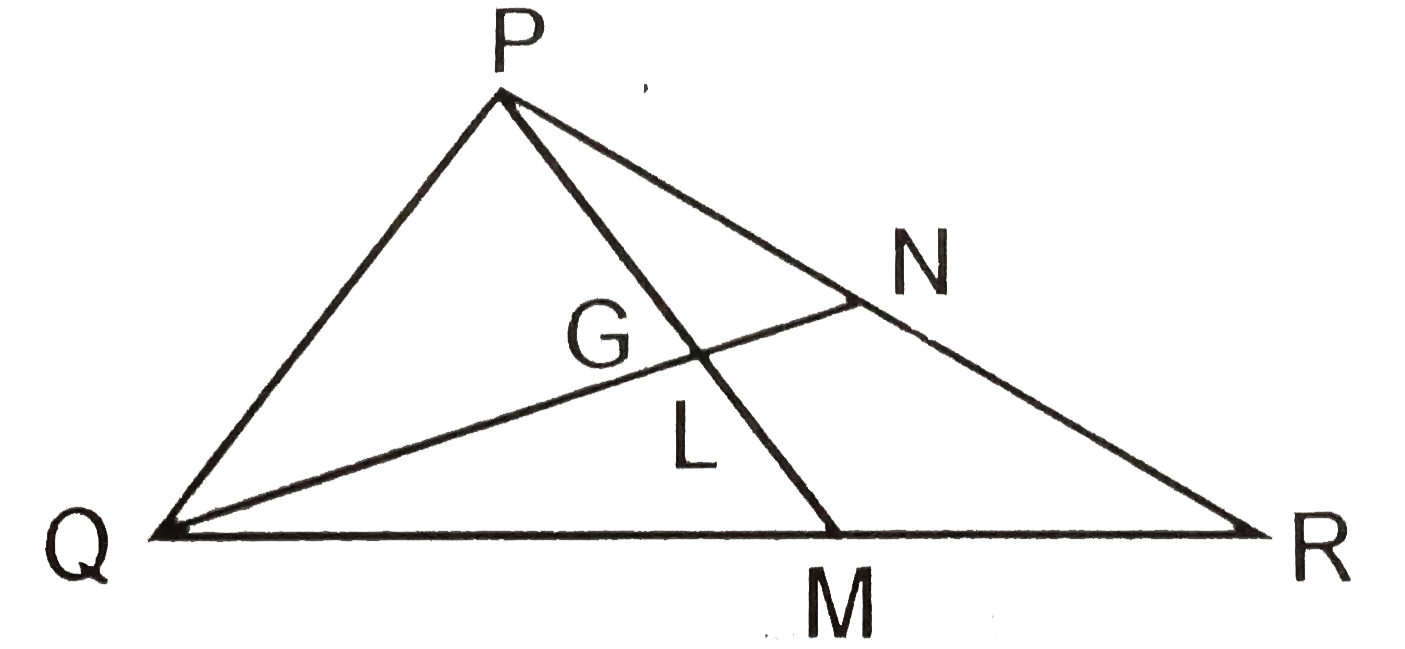
Let QR=p, PR=q, PQ=r
Given p2+q2=5r2
Now QG2+GM2=(2QN3)2+(PM2)2
=4QN29+PM29
=19[4.14(2r2+2p2−q2)+14(2r2+2p2−q2)]
p24=QM2
Hence Angle QGM is 90∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
PQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
A32B52C2DNone of these
Construct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
View SolutionIn a triangle PQR, S and T are points on QR and PR respectively, such that QS=3SR and PT=4TR. Let M be the point of intersection of PS and QT. Determine the ratio QM:MT
View SolutionIn a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
View SolutionConstruct a triangle PQR in which QR=4.7 cm PR−PQ=2.3cm and ∠Q−∠R=50∘.
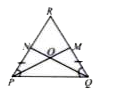
View SolutionIn the figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIn a triangle PQR, right angled at Q. PQ=5 cm, QR=12 cm. Find the length of QM , if M is the mid point of PR .
View SolutionPQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View Solution
