Consider the parabola x2+4y=0. Let P(a,b) be any fixed point inside the parabola and let S be the focus of the parabola. Then the minimum value at SQ+PQ as point Q moves on the parabola is (a) |1−a| (b) |ab|+1 (c) √a2+b2 (d) 1−bSolution in Bengali
|1−a|
|ab|+1
√a2+b2
1−b
The correct Answer is:D
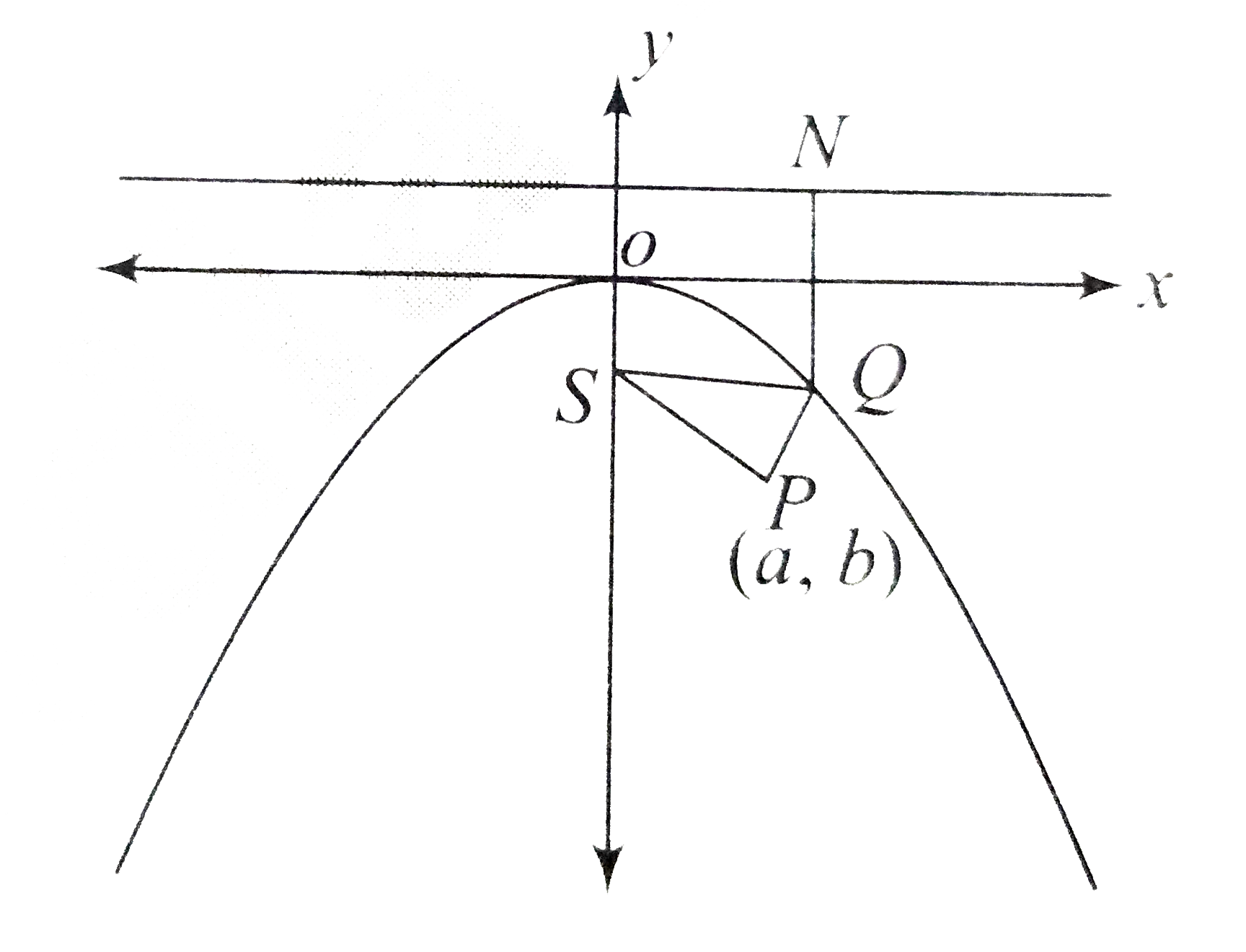
Let the foot of perpendicular from Q to the directrix be N.
SQ+PQ=QN+PQ is minimum when P, Q and N are collinear. So, minimum value of SQ+PQ=PN=1−b
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
- PARABOLABOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
A family of curve S is given by S≡x2+2xy+y2−4x(1−λ)−4y(1+λ)+4, then S=0 represents (a) pair of straight line ∀λ∈R (b) straight line for exactly one value of λ (c) parabola ∀λ∈R−{0} (d) ellipse for three values of λ
View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
View SolutionIf cos−1.x2+cos−1.y3=π6, then prove that x24−xy2√3+y29=14
View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionGiven are six 0's, five 1's and four 2's . Consider all possible permutations of all these numbers. [A permutations can have its leading digit 0].
How many permutations have the first 0 preceding the first 1 ?
(a) 15C4×10C5 (b) 15C5×10C4 (c) 15C6×10C5 (d) 15C5×10C5
View SolutionThe sraight line 3x-4y+c=0 Intersects the parabola x^(2)=4y at the points A and B Ifthe tangents to the parabola at A and B are perpendicular,then c=
View SolutionConsider two parabola y=x^(2)-x+1 and y=x^(2)+x+(1)/(2), the parabola y=-x^(2)+x+(1)/(2) is fixed and parabola y=-x^(2)+1 rolls without slipping around the fixed parabola,then the locus of the focus of the moving parabola is
View SolutionA particle moves on the parabola y2=4ax. Its distance from the focus is minimum for the following values of x (A) −1 (B) 0 (C) 1 (D) a
View SolutionConsider the parabola x2+4y=0. Let P(a,b) be any fixed point inside the parabola and let S be the focus of the parabola. Then the minimum value at SQ+PQ as point Q moves on the parabola is
View SolutionConsider a parabola x2−4xy+4y2−32x+4y+16=0.
The focus of the parabola (P) is
View Solution3 point O(0,0),P(a,a2),Q(−b,b2)(a>0,b>0) are on the parabola y=x2. Let S1 be the area bounded by the line PQ and parabola let S2 be the area of the ΔOPQ, the minimum value of S1/S2 is
View SolutionConsider the parabola y2=4x .A=(4,-4) and B=(9,6) "be two fixed point on the parabola"." Let 'C' be a moving point on the parabola between "A" and "B" such that the area of the triangle ABC is maximum then the co-ordinate of 'C' is
View SolutionLet tangent PQ and PR are drawn from the point P(−2,4) to the parabola y2=4x. If S is the focus of the parabola y2=4x, then the value (in units) of RS+SQ is equal to
View SolutionThe equation of a tangent to the parabola y2=8xisy=x+2 . The point on this line from which the other tangent to the parabola is perpendicular to the given tangent is (1) (−1,1) (2) (0,2) (3) (2,4) (4) (−2,0)
View SolutionConsider the parabola x2+4y=0. Let P(a,b) be any fixed point inside the parabola and let S be the focus of the parabola. Then the minimum value at SQ+PQ as point Q moves on the parabola is (a) |1−a| (b) |ab|+1 (c) √a2+b2 (d) 1−b
View Solution
