Draw the graph of f(x)=|x|−|2x−3|. Find the range of the function. Solution in Tamil
Function f(x)=|2x−1|+|2x−3| changes definition where 2x−1=0and2x−3=0orx=1/2andx=3/2.
Thus, we find the function in each of the intervals (−∞,1/2),(1/2,3/2)and(3/2,∞).
∴ f(x)=|2x−1|+|2x−3|=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩1−2x+3−2x,x<122x−1+3−2x,12≤x≤322x−1+2x−3,x>32
=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩4−4x,x<122,12≤x≤324x−4,x>32
Now we can draw the graph of each function in respective intervals.
Alternative method :
Since the graph of the function is linear in eah of the reagions (−∞,1/2),(1/2,3/2)and(3/2,∞), we need to check the values of the function at some particular values of x to draw the graph in each region.
f(1/2)=2
f(3/2)2
f(0)=4
f(2)=3+1=4
Thus, we plot the points A(0,4),B(1/2,2),C(3/2,2)andD(2,4). Plotting these points and connecting with the straight line, we have the following graph.
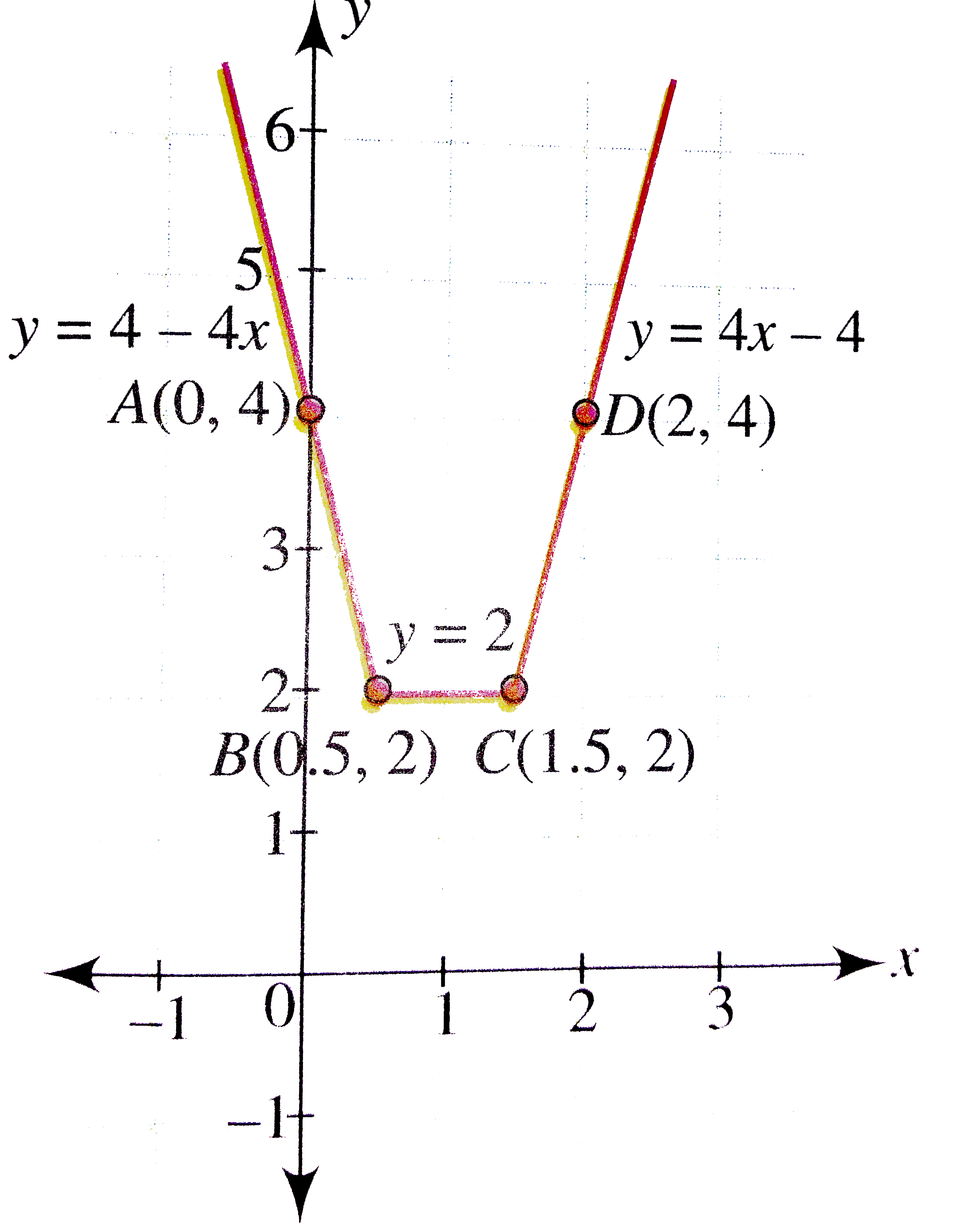
From the graph, the range of the function is [2,∞).
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of the function f(x)=2x-|x|
View SolutionDraw the graph of the function f(x)=max.sinx,cos2x,x∈[0,2π]. Write the equivalent definition of f(x) and find the range of the function.
View SolutionDraw the graph of following function and find range (R_(f)) of f(x)=|x-2|+|2-x|AA-3<=x<=3
View SolutionDraw the graph of f(x)=|2x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of the function, f(x) = 2x - 5.
View SolutionDraw the graph of f(x)=(2^(x))/(2^([x])) where [.] represents greatest integer function and find the domain and range.
View SolutionDraw the graph of the function f :R → R defined by
f(x)=x3,x∈R
find its domain and range
View SolutionDraw the graph of the function f(x)=max{sinx,cos2x},x∈[0,2π]. Write the equivalent definition of f(x) and find the range of the function.
View SolutionDraw the graph of f(x)=|2x−1|+|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x|−|2x−3|. Find the range of the function.
View SolutionDraw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
View Solution
