Doubtnut Promotions Sticky

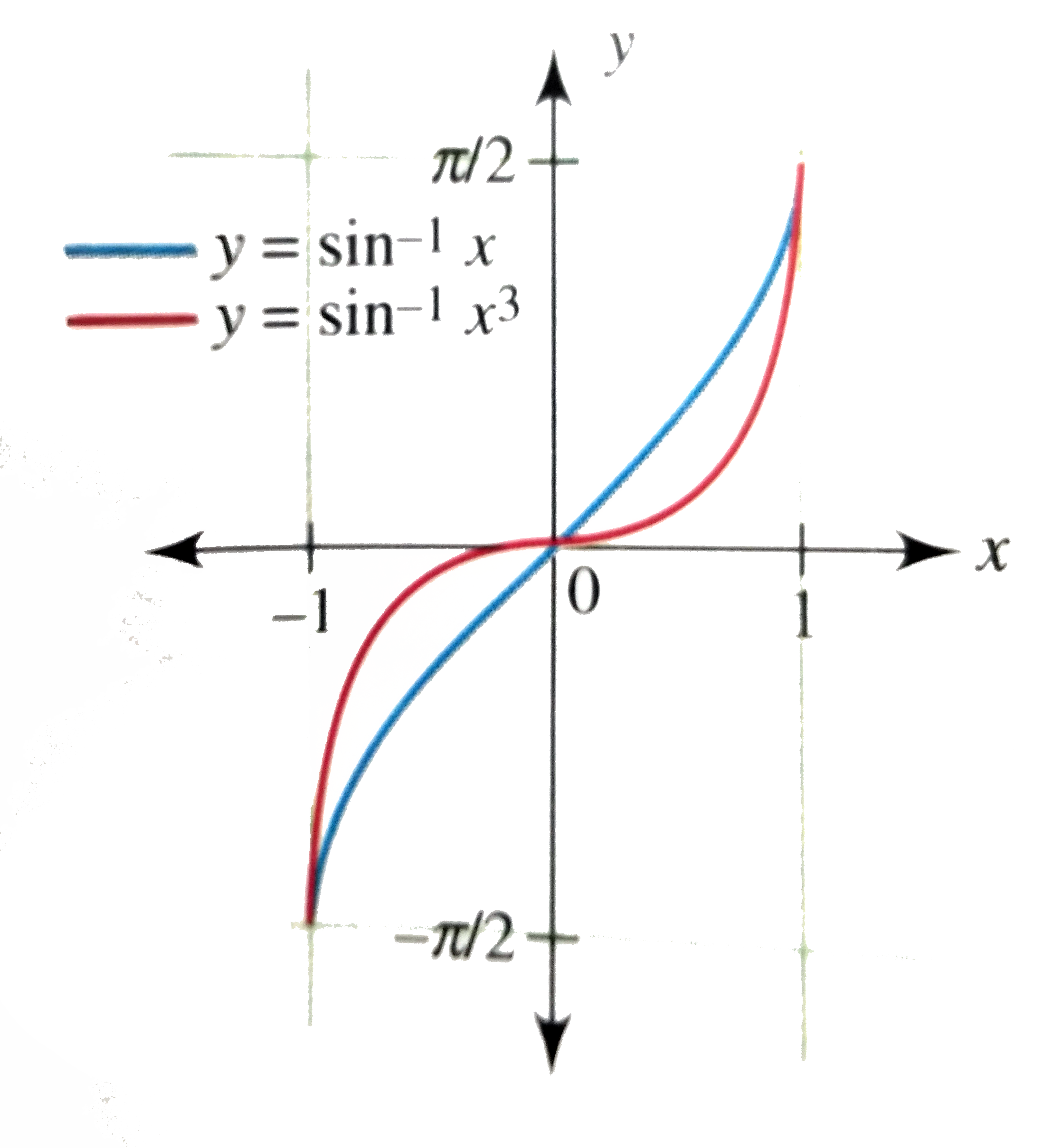
Draw the graph of y=sin−1x3 and compare wire the graph of y=sin−1x.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=sin−1x3
We must have−1≤x3≤1∴−1≤x≤1
Also sin−1x3 is increasing as sin−1 x and x3 both are increasing
f(−1)=sin−1(−1)3=sin−1(−1)=−π/2
f(−1)=sin−1(−1)3=sin−1(−1)=π/2
f(0)=sin−10=0
f(1)=sin−1=π/2
For −1≤x<0,x<x3∴sin−1x<sin−1x3 heance the graph of y=sin−1x3 lies below the graph of y=sin−1x.
For −1≤x<0,x<x3∴sin−1x<sin−1x3 heance the graph of y=sin−1x3 lies above the graph of y=sin−1x.
Therefore graph of both functions ar as shown in the followin figure.
ocr_image

|