E and F are respectively the midpoints of nonparallel sides AD and BC of a trapezium ABCD. Prove that EF||AB.
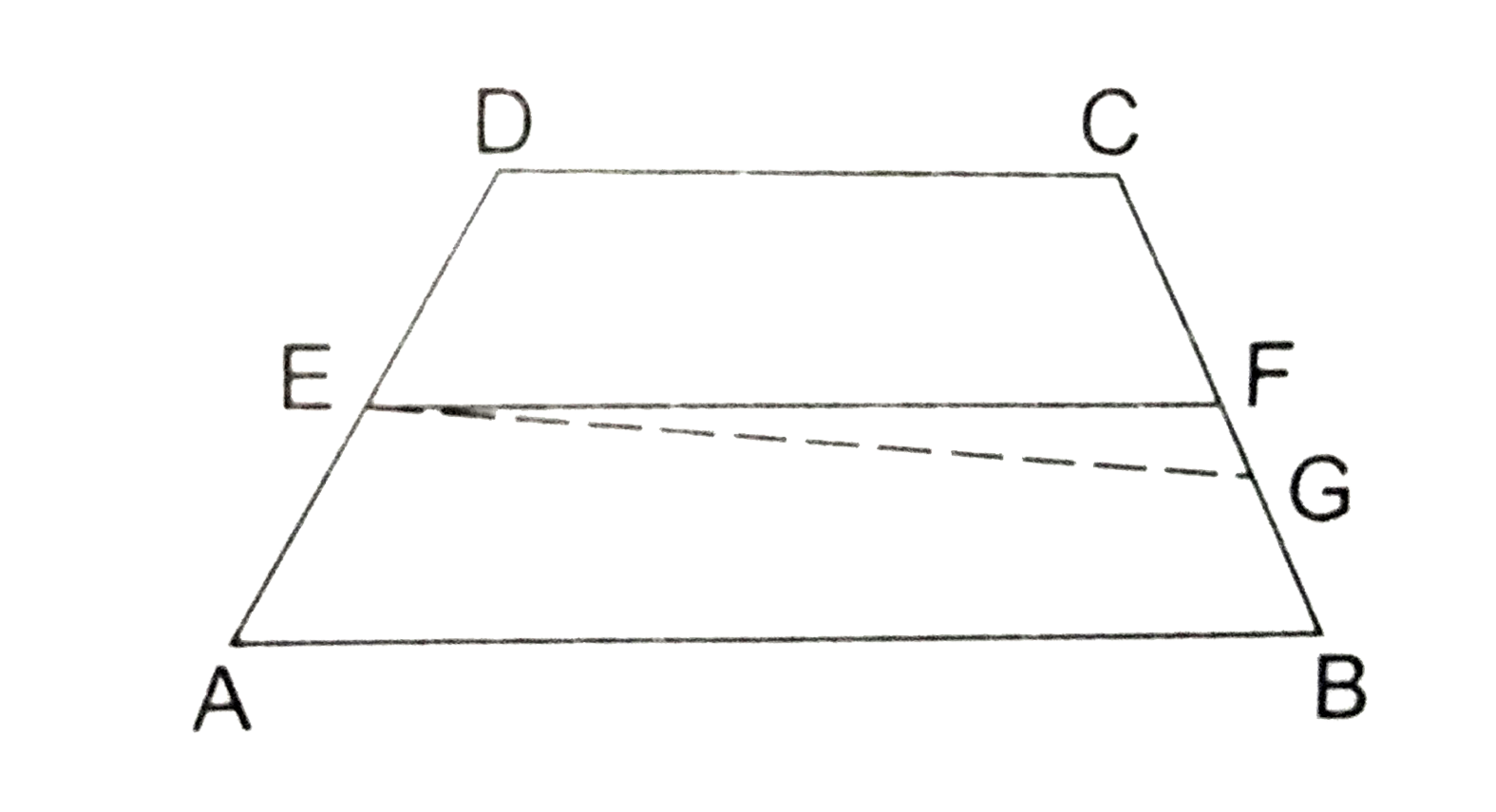
Let ABCD be a trapezium in which AB||DC. Let E and F be midpoints of AD and BC respectively. E and F are joined.
We have to show that EF || AB.
If possible. Let EF be not parallel to AB then draw EG||AB, meeting BC at G.
Now, AB||EG||DC and the transversal AD cuts them at A, E, D respectively. such that AE = ED.
Also, BGC is the other transversal cutting AB, EG and DC at B, G and C respectively.
BG = GC (by intercept theorem).
This shows that G is the midpoint of BC.
Hence, G must coincide with F [ F is the midpoint of BC].
Thus, our supposition is wrong.
Hence, EF || AB.
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
E and F are respectively the midpoints of the non-parallel sides AD and BC of a trapezium ABCD. Prove that
(i) EF∣∣AB,
(ii) EF=12(AB+CD).
View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View Solution
Knowledge Check
If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD10/3, 9 and 12 cmIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD103, 9 and 12 cmABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
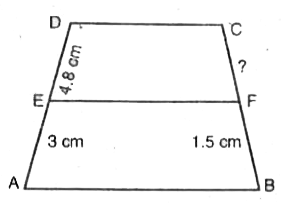 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of these
ABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionIn a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionThe line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View Solution
