Fide the area bounded by y=sin−1(sinx) and the x-axis for x∈[0,100π].
In the graph of y=sin−1(sinx),x∈[0,100π], there are 50 triangles above the x-axis and 50 triangles below the x-axis.
Therefore required area, A=100× Area of one triangle as shown in the following figure
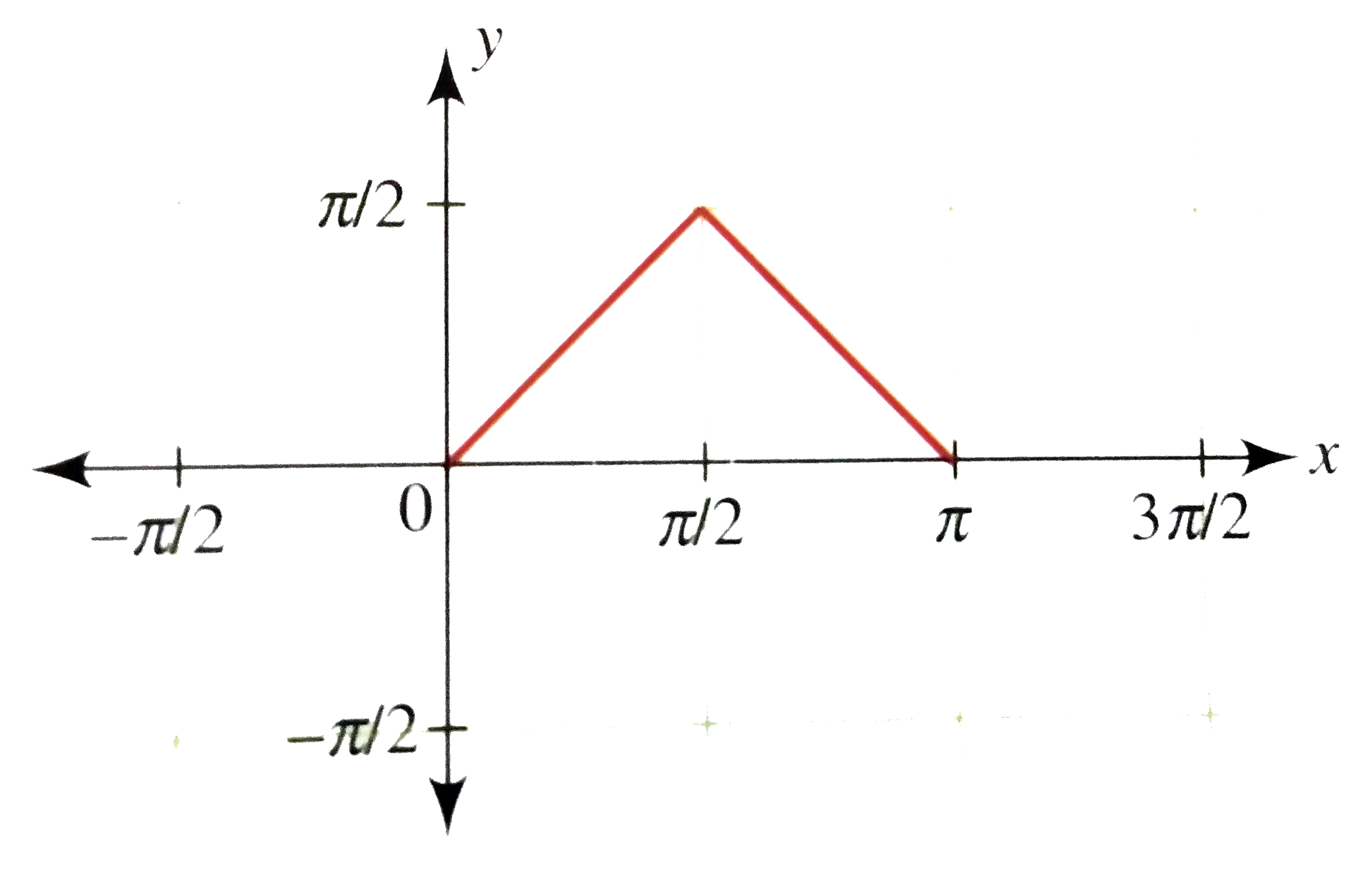
∴ A=100×(12×π2×π)=25π2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.181videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION78videos
GRAPHICAL TRANSFORMATIONS
Similar Questions
Find the area bounded by y=sin−1(sinx) and x-axis for x∈[0,100π]
View SolutionFind the area bounded by y=sin−1(sinx) and x-axis for x in [0,100π]
View SolutionFind the area bounded by y=sin−1x,y=cos−1x ,and the X-axis.
View SolutionThe area bounded by y=−x2+1 and the x-axis is
View SolutionThe area bounded by the curve y=sin2x−2sinx and the x-axis, where x∈[0,2π], is
View SolutionFind the area bounded by y=∣∣∣sinx−12∣∣∣andy=1 for x∈[0,π]
View SolutionFind the area bounded by y = sin x and axis of x in (0,π)
View SolutionThe area bounded by the curve y=sin−1(sinx) and the x - axis from x=0 to x=4π is equal to the area bounded by the curve y=cos−1(cosx) and the x - axis from x=−π to x=a, then the value of a is equal to
View SolutionFind the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
View SolutionThe area bounded by y=|sinx|, X-axis and the lines |x|=π is
View Solution

