Find the frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46.
To find the missing frequencies in the frequency distribution given that the mean is 1.46, we can follow these steps:
1. Understand the Given Information:
- We know the mean of the distribution is 1.46.
- The total sum of frequencies is 200.
- We need to find two missing frequencies, which we will denote as a and b.
2. Set Up the First Equation:
- Since the total sum of frequencies is 200, we can write:
46+a+b+25+10+5=200
- Calculate the sum of the known frequencies:
46+25+10+5=86
- Therefore, we have:
a+b=200−86=114(Equation 1)
3. Set Up the Second Equation Using the Mean:
- The formula for the mean is given by:
Mean=∑(xifi)∑fi
- Here, xi represents the mid-values of the classes, and fi represents the frequencies. We can express the mean as:
1.46=0⋅46+1⋅a+2⋅b+3⋅25+4⋅10+5⋅5200
- Calculate the contributions from the known frequencies:
0+a+2b+75+40+25=a+2b+140
- Thus, we can write:
1.46=a+2b+140200
- Multiply both sides by 200:
1.46⋅200=a+2b+140
- Calculate 1.46⋅200:
292=a+2b+140
- Rearranging gives us:
a+2b=292−140=152(Equation 2)
4. Solve the System of Equations:
- Now we have two equations:
- Equation 1: a+b=114
- Equation 2: a+2b=152
- Subtract Equation 1 from Equation 2:
(a+2b)−(a+b)=152−114
- This simplifies to:
b=38
5. Substitute Back to Find a:
- Substitute b=38 back into Equation 1:
a+38=114
- Solving for a:
a=114−38=76
6. Final Frequencies:
- The missing frequencies are:
- Frequency of 1 (denoted as a): 76
- Frequency of 2 (denoted as b): 38
Summary of the Solution:
- Frequency of 1: 76
- Frequency of 2: 38
- We know the mean of the distribution is 1.46.
- The total sum of frequencies is 200.
- We need to find two missing frequencies, which we will denote as a and b.
- Since the total sum of frequencies is 200, we can write:
46+a+b+25+10+5=200
- Calculate the sum of the known frequencies:
46+25+10+5=86
- Therefore, we have:
a+b=200−86=114(Equation 1)
- The formula for the mean is given by:
Mean=∑(xifi)∑fi
- Here, xi represents the mid-values of the classes, and fi represents the frequencies. We can express the mean as:
1.46=0⋅46+1⋅a+2⋅b+3⋅25+4⋅10+5⋅5200
- Calculate the contributions from the known frequencies:
0+a+2b+75+40+25=a+2b+140
- Thus, we can write:
1.46=a+2b+140200
- Multiply both sides by 200:
1.46⋅200=a+2b+140
- Calculate 1.46⋅200:
292=a+2b+140
- Rearranging gives us:
a+2b=292−140=152(Equation 2)
- Now we have two equations:
- Equation 1: a+b=114
- Equation 2: a+2b=152
- Subtract Equation 1 from Equation 2:
(a+2b)−(a+b)=152−114
- This simplifies to:
b=38
- Substitute b=38 back into Equation 1:
a+38=114
- Solving for a:
a=114−38=76
- The missing frequencies are:
- Frequency of 1 (denoted as a): 76
- Frequency of 2 (denoted as b): 38
- Frequency of 1: 76
- Frequency of 2: 38
Topper's Solved these Questions
Similar Questions
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. N⊙ofant(x) 0 1 2 3 4 5 TotalFrequency(f): 46 ? ? 25 10 5 200
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50. x : 10 30 50 70 90 f : 17 f1 32 f2 19 Total 120.
View Solution
Knowledge Check
Find the missing frequency in the following distribution, if it is known that the mean of the distribution is 50.16
 Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50. f=17,f1=32,f2=19 Total 120
View SolutionFind mode of the following frequency distribution.
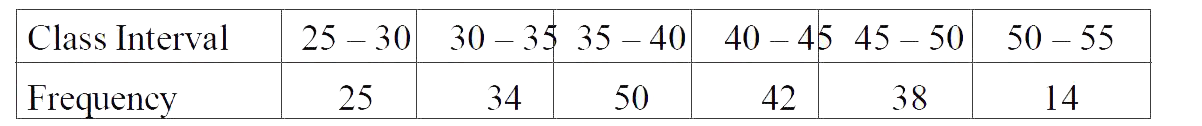
View SolutionFind the median marks for the following frequency distribution :

View SolutionConsider the following frequency distribution :

What is the median for the distribution?
View SolutionFind the mean marks from the following frequency distribution

View SolutionThe mean of the following frequency distribution is 50 :

View SolutionConsider the following frequency distribution
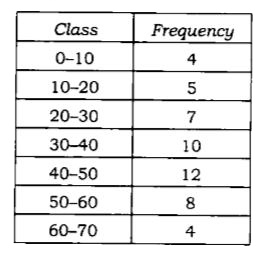
What is the median of the distribution?
View Solution