Find the mean deviation from the mean for the following data: 5 2 9 10 12 15 8 6 2 2 2 6
To find the mean deviation from the mean for the given data, we will follow these steps:
Step 1: Organize the Data
We have two sets of data points. Let's denote the first set as x1 and the second set as x2.
- x1=(5,2,9,10,12,15)
- x2=(8,6,2,2,2,6)
Step 2: Create a Frequency Table
We can create a frequency table for the data:
| xi | Frequency fi |
|-----------|---------------------|
| 2 | 3 |
| 5 | 1 |
| 6 | 2 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 12 | 1 |
| 15 | 1 |
Step 3: Calculate fi×xi
Now, we will calculate fi×xi for each data point:
| xi | Frequency fi | fi×xi |
|-----------|---------------------|-----------------------|
| 2 | 3 | 2×3=6 |
| 5 | 1 | 5×1=5 |
| 6 | 2 | 6×2=12 |
| 8 | 1 | 8×1=8 |
| 9 | 1 | 9×1=9 |
| 10 | 1 | 10×1=10|
| 12 | 1 | 12×1=12|
| 15 | 1 | 15×1=15|
Step 4: Sum of Frequencies and fi×xi
Now, we will sum the frequencies and the products:
- Total frequency ∑fi=3+1+2+1+1+1+1+1=11
- Total ∑(fi×xi)=6+5+12+8+9+10+12+15=67
Step 5: Calculate the Mean
Using the formula for the mean:
Mean=∑(fi×xi)∑fi=6711≈6.09
Step 6: Calculate the Mean Deviation
Next, we will calculate the mean deviation from the mean. The formula for mean deviation is:
Mean Deviation=∑fi|xi−Mean|∑fi
Now we will calculate |xi−Mean| for each xi:
| xi | Frequency fi | |xi−Mean| | fi×|xi−Mean| |
|-----------|---------------------|---------------------------|----------------------------------|
| 2 | 3 | |2−6.09|=4.09 | 3×4.09=12.27 |
| 5 | 1 | |5−6.09|=1.09 | 1×1.09=1.09 |
| 6 | 2 | |6−6.09|=0.09 | 2×0.09=0.18 |
| 8 | 1 | |8−6.09|=1.91 | 1×1.91=1.91 |
| 9 | 1 | |9−6.09|=2.91 | 1×2.91=2.91 |
| 10 | 1 | |10−6.09|=3.91 | 1×3.91=3.91 |
| 12 | 1 | |12−6.09|=5.91 | 1×5.91=5.91 |
| 15 | 1 | |15−6.09|=8.91 | 1×8.91=8.91 |
Step 7: Sum of fi×|xi−Mean|
Now we will sum fi×|xi−Mean|:
∑(fi×|xi−Mean|)=12.27+1.09+0.18+1.91+2.91+3.91+5.91+8.91=36.18
Step 8: Calculate the Mean Deviation
Finally, we can calculate the mean deviation:
Mean Deviation=36.1811≈3.29
Final Answer
The mean deviation from the mean for the given data is approximately 3.29.
---
We have two sets of data points. Let's denote the first set as x1 and the second set as x2.
- x2=(8,6,2,2,2,6)
We can create a frequency table for the data:
|-----------|---------------------|
| 2 | 3 |
| 5 | 1 |
| 6 | 2 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 12 | 1 |
| 15 | 1 |
Now, we will calculate fi×xi for each data point:
|-----------|---------------------|-----------------------|
| 2 | 3 | 2×3=6 |
| 5 | 1 | 5×1=5 |
| 6 | 2 | 6×2=12 |
| 8 | 1 | 8×1=8 |
| 9 | 1 | 9×1=9 |
| 10 | 1 | 10×1=10|
| 12 | 1 | 12×1=12|
| 15 | 1 | 15×1=15|
Now, we will sum the frequencies and the products:
- Total ∑(fi×xi)=6+5+12+8+9+10+12+15=67
Using the formula for the mean:
Next, we will calculate the mean deviation from the mean. The formula for mean deviation is:
|-----------|---------------------|---------------------------|----------------------------------|
| 2 | 3 | |2−6.09|=4.09 | 3×4.09=12.27 |
| 5 | 1 | |5−6.09|=1.09 | 1×1.09=1.09 |
| 6 | 2 | |6−6.09|=0.09 | 2×0.09=0.18 |
| 8 | 1 | |8−6.09|=1.91 | 1×1.91=1.91 |
| 9 | 1 | |9−6.09|=2.91 | 1×2.91=2.91 |
| 10 | 1 | |10−6.09|=3.91 | 1×3.91=3.91 |
| 12 | 1 | |12−6.09|=5.91 | 1×5.91=5.91 |
| 15 | 1 | |15−6.09|=8.91 | 1×8.91=8.91 |
Now we will sum fi×|xi−Mean|:
Finally, we can calculate the mean deviation:
The mean deviation from the mean for the given data is approximately 3.29.
Topper's Solved these Questions
Similar Questions
Find the mean deviation from the mean for the followinng data:
 View Solution
View SolutionFind the mean deviation from the median for the following data:
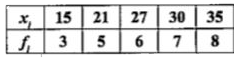 View Solution
View SolutionFind the mean deviation for the mean for the following data:
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the mean for the following data.
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about mean for the following data:
 View Solution
View SolutionFind the mean and standard deviation from the following data :
 View Solution
View SolutionMean deviation from mean of the data is
 View Solution
View Solution

