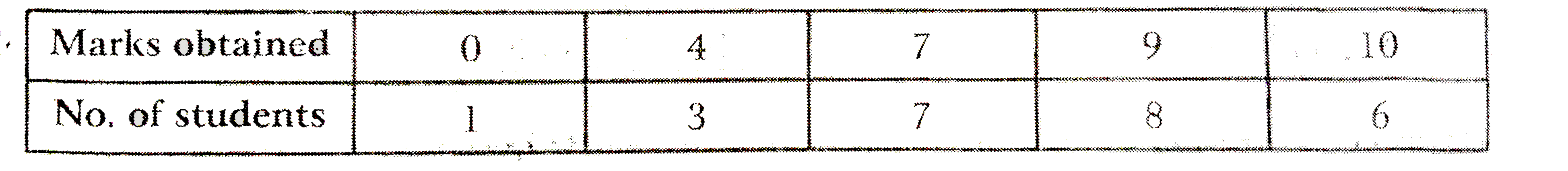Following table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
To solve the problem step by step, we will find the probabilities for each of the three parts of the question.
Given Data:
- Total number of students = 90
Marks Distribution:
| Marks | No. of Students |
|---------|-----------------|
| 0-20 | 7 |
| 20-30 | 10 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 20 |
| 60-70 | 15 |
| 70-100 | 8 |
(i) Probability that marks scored by a student is at most 60 marks:
To find this probability, we need to sum the number of students who scored 60 marks or less.
- Students scoring 0-20: 7
- Students scoring 20-30: 10
- Students scoring 30-40: 10
- Students scoring 40-50: 20
- Students scoring 50-60: 20
Total students scoring at most 60 marks:
7+10+10+20+20=67
Probability:
P(at most 60 marks)=Number of students scoring at most 60Total number of students=6790
(ii) Probability that marks scored by a student is at least 60 marks:
To find this probability, we need to sum the number of students who scored 60 marks or more.
- Students scoring 60-70: 15
- Students scoring 70-100: 8
Total students scoring at least 60 marks:
15+8=23
Probability:
P(at least 60 marks)=Number of students scoring at least 60Total number of students=2390
(iii) Probability that marks scored by a student is not more than 50 marks:
To find this probability, we need to sum the number of students who scored 50 marks or less.
- Students scoring 0-20: 7
- Students scoring 20-30: 10
- Students scoring 30-40: 10
- Students scoring 40-50: 20
Total students scoring not more than 50 marks:
7+10+10+20=47
Probability:
P(not more than 50 marks)=Number of students scoring not more than 50Total number of students=4790
Final Answers:
1. Probability that marks scored by a student is at most 60 marks: 6790
2. Probability that marks scored by a student is at least 60 marks: 2390
3. Probability that marks scored by a student is not more than 50 marks: 4790
- Total number of students = 90
| Marks | No. of Students |
|---------|-----------------|
| 0-20 | 7 |
| 20-30 | 10 |
| 30-40 | 10 |
| 40-50 | 20 |
| 50-60 | 20 |
| 60-70 | 15 |
| 70-100 | 8 |
To find this probability, we need to sum the number of students who scored 60 marks or less.
- Students scoring 20-30: 10
- Students scoring 30-40: 10
- Students scoring 40-50: 20
- Students scoring 50-60: 20
7+10+10+20+20=67
P(at most 60 marks)=Number of students scoring at most 60Total number of students=6790
To find this probability, we need to sum the number of students who scored 60 marks or more.
- Students scoring 70-100: 8
15+8=23
P(at least 60 marks)=Number of students scoring at least 60Total number of students=2390
To find this probability, we need to sum the number of students who scored 50 marks or less.
- Students scoring 20-30: 10
- Students scoring 30-40: 10
- Students scoring 40-50: 20
7+10+10+20=47
P(not more than 50 marks)=Number of students scoring not more than 50Total number of students=4790
1. Probability that marks scored by a student is at most 60 marks: 6790
2. Probability that marks scored by a student is at least 60 marks: 2390
3. Probability that marks scored by a student is not more than 50 marks: 4790
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The marks scored by 10 students in a monthly test are:
9, 13, 17, 6, 8, 13, 11, 10, 5, 9
The median marks areA9B10C9.5D10.5
Marks of 40 student in a test out of maximum 50 marks are as follow :
 View Solution
View SolutionThe following table gives the marks scored by 100 students in an entrance examination. Marks: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 No. of Students (Frequency): 4 10 16 22 20 18 8 2 Represent this data in the form of a histogram.
View SolutionThe following table gives the marks scored by 378 students in an entrance examination : Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 No. of Students 3 12 36 76 97 85 39 12 12 6 From this table form (i) less than series, and (ii) the more than series.
View SolutionFollowing are the marks obtained by 9 student in a mathematics test
50,69,20,33,53,39,40,65,59,
The mean deviation from the median isView SolutionThe following table shows the marks scored by 140 students in an examination of a certain paper: Marks: 0-10 10-20 20-30 30-40 40-50 No. of students: 20 24 40 36 20 Calculate the average marks by using the assumed mean deviation method.
View SolutionCompute mean deviation from mean of the following distribution: Marks 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of students 8 10 15 2 20 18 9 5
View SolutionIf for somex∈R, the frequency distribution of the marks obtained by 20 students in a test is:

Then the mean of the marks is:View Solution