From a point $P$ , two tangents $P A$ and $P B$ are drawn to a circle $C (O, r)$ . If $O P = 2 r$ , show that $Δ A P B$ is equilateral.

Video Solution

Text Solution

Verified by Experts

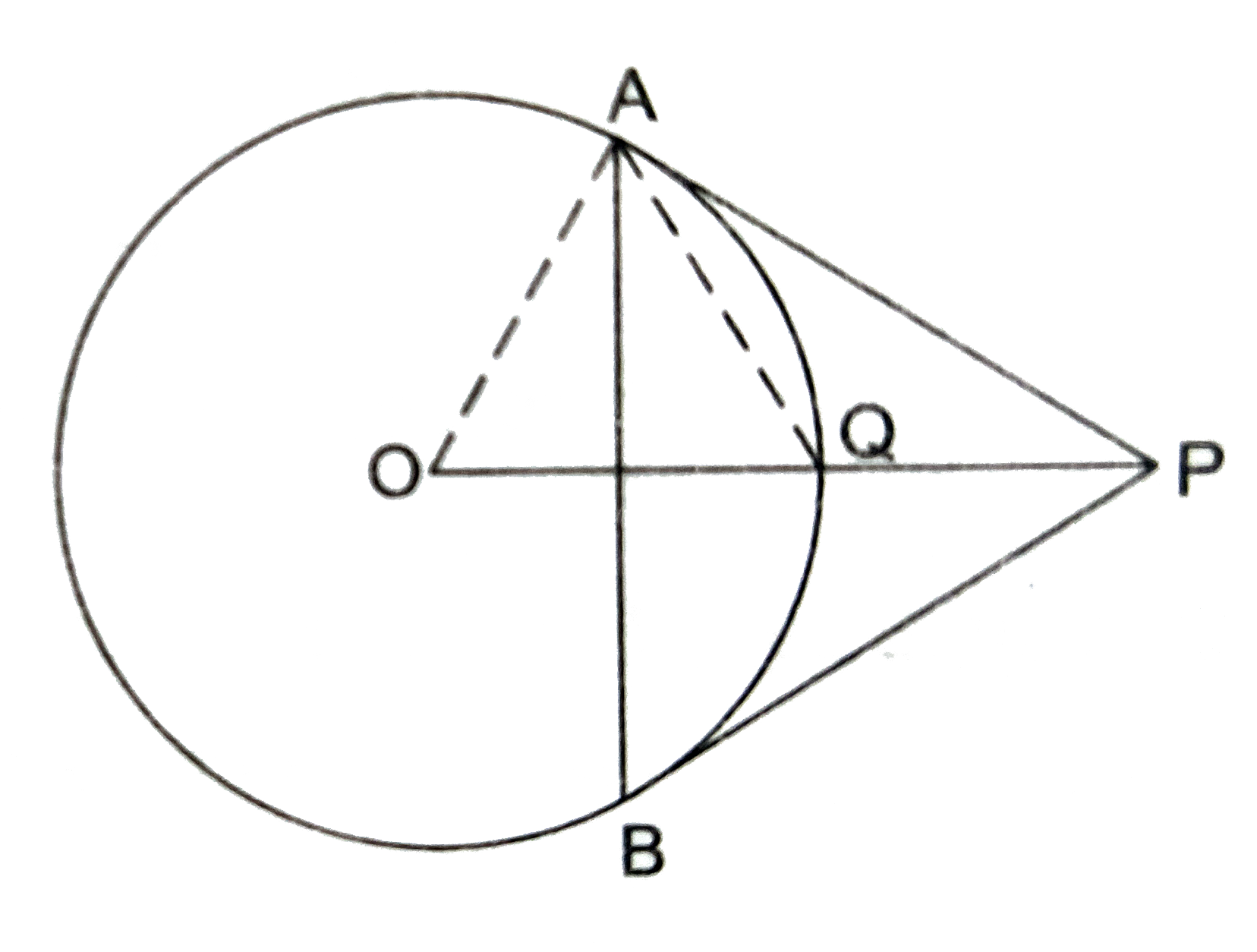
Let $O P$ meet the circle at $Q$ .
Join $O A$ and $A Q$ .
Clearly, $O A ⊥ A Π m p l i e s ∠ O A P = 90^{\circ}$ [radius through the point of contact is perpendicular to the tangent].
Now, $O Q = Q P = r$
Thus, $Q$ is the midpoint of the hypotenuse $O P$ of $Δ O A P$ .
So, $Q$ is equidistant from $O$ , $A$ and $P$ .
$∴ Q A = O Q = Q P = r$
$\Rightarrow O A = O Q = Q A = r$
$\Rightarrow Δ A O Q$ is equilateral
$\Rightarrow ∠ A O Q = 60^{\circ}$ [ $∵$ each angle of an equilateral triangle is $60^{\circ}$ ]
$\Rightarrow ∠ A O P = 60^{\circ}$
$\Rightarrow ∠ A P O = 30^{\circ}$ [ $∵ ∠ A O P + ∠ O A P + ∠ A P O = 180^{\circ}$ ]
$\Rightarrow ∠ A P B = 2 ∠ A P O = 60^{\circ}$ .
Also, $P A = P B \Rightarrow ∠ P A B = ∠ P B A = 60^{\circ}$
Hence, $Δ P A B$ is an equilateral triangle.

Updated on:21/07/2023

From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then $∠ A P B$ is
A $45^{\circ}$
B $90^{\circ}$
C $30^{\circ}$
D $60^{\circ}$
From a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then $∠ A P B$ is
A $60^{\circ}$
B $45^{\circ}$
C $90^{\circ}$
D $30^{\circ}$