Given (where {} and [] denotes the fractional part and the integral part functions respectively). Then which of the following statements do/does not hold good?Solution in Punjabi
Continuous at x = 0
Irremovable discontinuity at x = 0
The correct Answer is:A, B, C
Step by step video & image solution for Given f(x)={{:(3-[cot^(-1)((2x^3-3)/(x^2))], x >0) ,({x^2}cos(e^(1/x)) , x<0):} (where {} and [] denotes the fractional part and the integral part functions respectively). Then which of the following statements do/does not hold good? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)11videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 43videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)50videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 83videos
COMPLEX NUMBERS
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.04:52View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
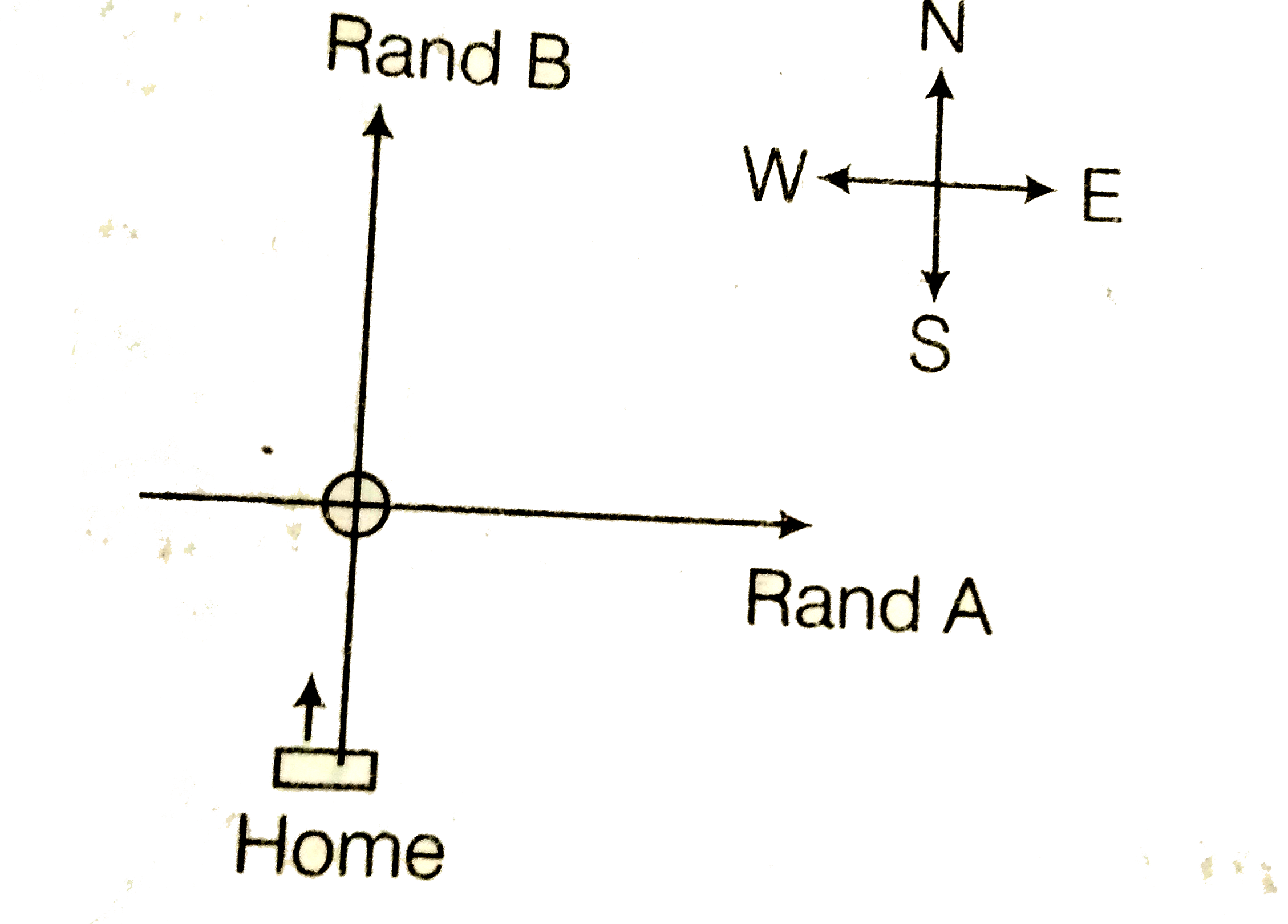
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous02:45View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
03:49View SolutionFind the modules of 2+3ι
05:42View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
05:59View SolutionGiven f(x)={3−[cot−1(2x3−3x2)]forx>0{x2}cos(e1x)forx<0 (where {} and [] denotes the fractional part and the integral part functions respectively). Then which of the following statements do/does not hold good? f(0−)=0 b. f(0+)=3 c. if f(0)=0 , then f(x) is continuous at x=0 d. irremovable discontinuity of f at x=0
07:02View SolutionThe number of integers in the range of the function f(x)=(x-[x])/(1+{x}) x(where [.] and {.} denote the integral part and fractional part functions respectively is
06:06View Solutionlim_(x rarr[a])(e^(x)-{x}-1)/({x}^(2)) Where {x} denotes the fractional part of x and [x] denotes the integral part of a.
03:16View SolutionConsider the function f(x)=(cos^(-1)(1-{x}))/(sqrt(2){x}); where {.} denotes the fractional part function,then
02:04View SolutionFor the function f(x)=e^(e^(x))-tan^(-1)x-3=0 which of the following holds good?
06:01View SolutionA function f(x)=x[1+((1)/(3))sin(In x^(2))],x!=0 integral part f(0)=0. Then the function
05:00View SolutionGiven f(x)=[log_a (a|[x]+[-x]|)^x((a^((2/(([x]+[-x])))/(|x|)-5))/(3+a^(1/(|x|))) for |x| !=0 ; a lt 1 and 0 for x=0 where [ ] represents the integral part function, then
04:28View SolutionDiscuss the continuity of the function f(x){(a^(2)[x]+{x}-1)/(2[x]+{x}),x!=0log_(e)a,x=0atx=0 denotes greatest integral part and {*} denotes fractional part function.
View SolutionIf [.] and {.} denote greatest and fractional part functions respectively and f(x)=⎧⎨⎩x(e[x]+|x|−2[x]+{2x})x≠0−1x=0 then
05:37View SolutionLet {x} and [x] denotes the fraction fractional and integral part of a real number (x), respectively. Solve ∣2x−1+=3[x]+2[x].
04:27View SolutionLet g(x)=tan−1|x|−cot−1|x|,f(x)=[x][x+1]{x},h{x}=|g(f(x))| then which of the following holds good? (where {*} denotes fractional part and {*} denotes the integral part)
05:17View Solution

