Question

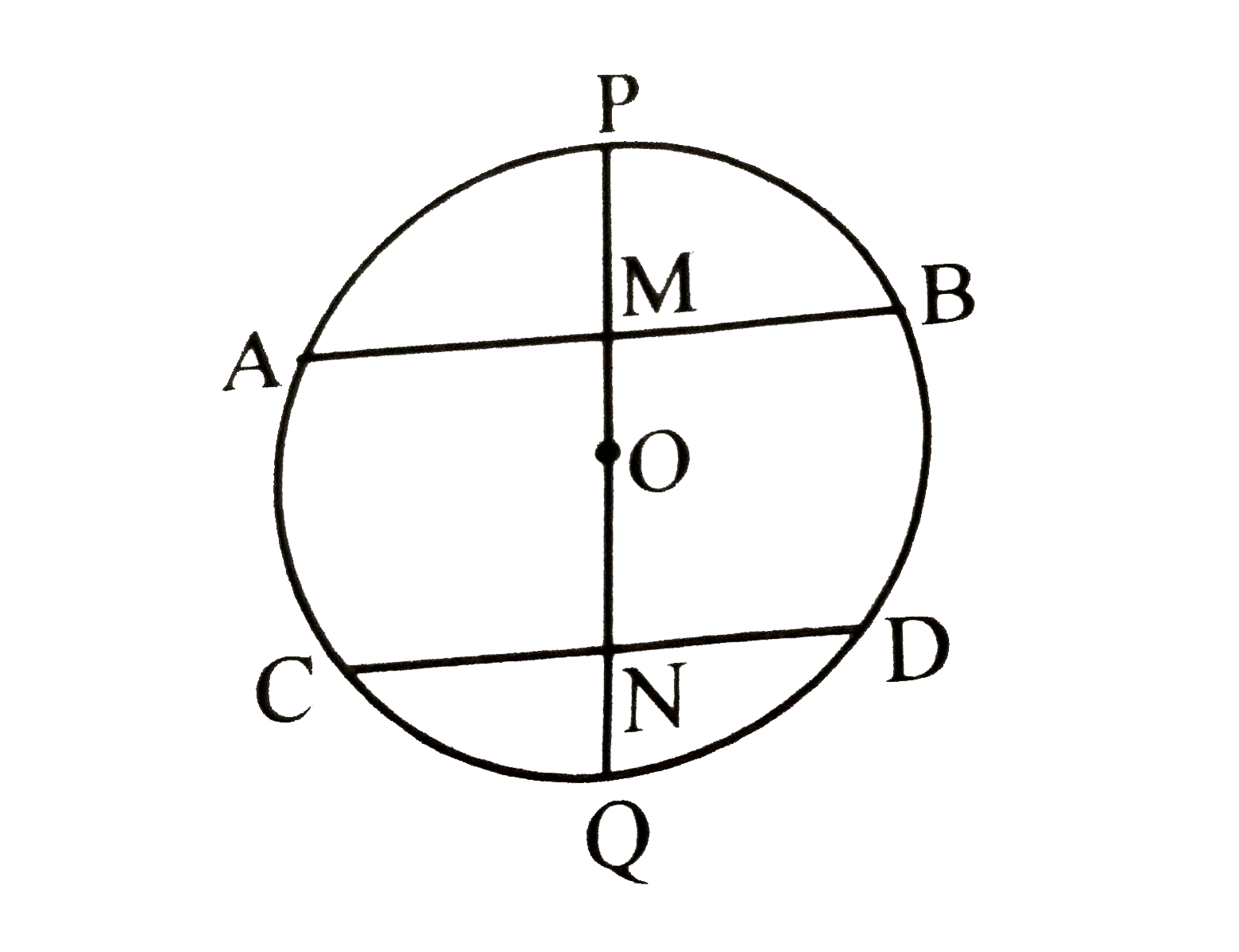
If a diameter of a circle bisects each of the two chords of a circle,
prove that the chords are parallel.

Explanation

There are two chords `AB` and `CD`, which are bisected by the diameter.
We have to prove that `AB` is parallel to `CD`.
Since `ON` bisects `CD,` therefore `ON` is perpendicular to `CD`.
(Perpendicular drawn from center of the circle to a chord, bisect the chord in equal parts)
Similarly, `OM` is perpendicular to `AB`
To prove that the two chords are parallel we need to show their alternative interior angles are equal.
Since, For chords `AB` and `CD`, `MN` act as a transversal.
Angle `AMN =` angle `MND` ( both are `90` degrees)
Hence, we can say both chords `AB` and `CD` are parallel to each other.