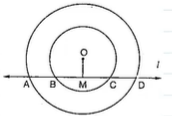
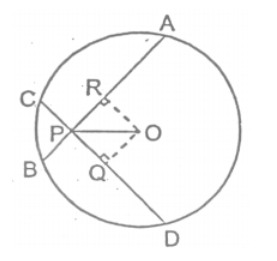
If a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
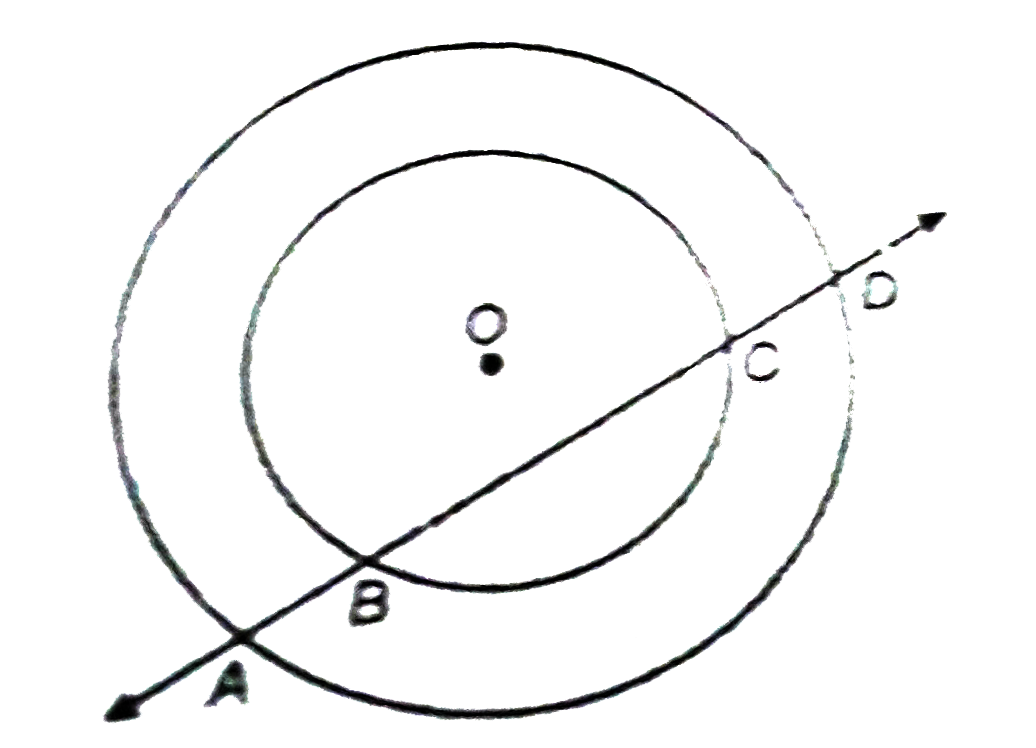
Let OP be the perpendicular from O on line l. since, the perpendicular from the centre of a circle to a chord bisects the chords.
Now, BC is the chord of the smaller circle and OP⊥BC .
∴AP=PC......(1)
Since, AD is a chord of the larger circle and OP⊥AD
∴AP=PD ......(2)
On subtracting eq. (1) from eq. (2), we get
AP−BP=PD⇒AB=CD
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D. then.
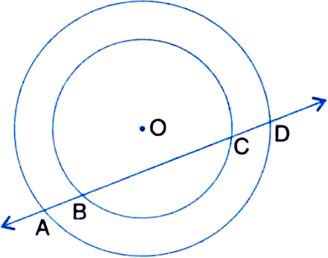 AAB=BDBCD=ACCAB=CDDNone
AAB=BDBCD=ACCAB=CDDNone
In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A,B,C and D . Show that AB=CD.
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionA straight line intersects thethree concentric circles at A, B, C. if the distance of line from the centre of the circles is 'P', prove that the area of the triangle formed by tangents to the circle at A, B, C is (12P.AB.BC.CA).
View SolutionIn Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
View SolutionGiven two concetric circles with centre O. A line cut the circle at A,B,C and D respectively. If AB=10cm, then find the length of CD.
View Solution