In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A, B, C and D . Show that AB=CD.
Let OM be perpendicular from Oonl∈e l
We know that perpendicular from the center of the circle to as a chord :bisects the chord
since BC is chord of the smaller circle
OM⊥BC
BM=CM....(i)
Again AD is chord of the larger circle and AM⊥AD
AM=DM...(II)
subtracting from (i) and (ii), AM−BM=DM−CM⇒AB=CDLet OM be perpendicular from O on line l
We know that perpendicular from the center of the circle to as a chord :bisects the chord
since BC is chord of the smaller circle
OM⊥BC
BM=CM....(i)
Again AD is chord of the larger circle and AM⊥AD
AM=DM...(II)
subtracting from (i) and (ii), AM−BM=DM−CM⇒AB=CD
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D. then.
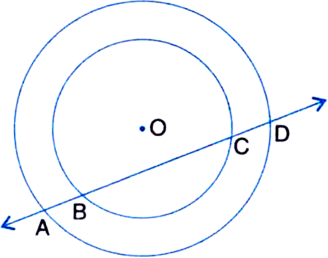 AAB=BDBCD=ACCAB=CDDNone
AAB=BDBCD=ACCAB=CDDNone - Question 2 - Select One
The radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
A20B24C30D34
If a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
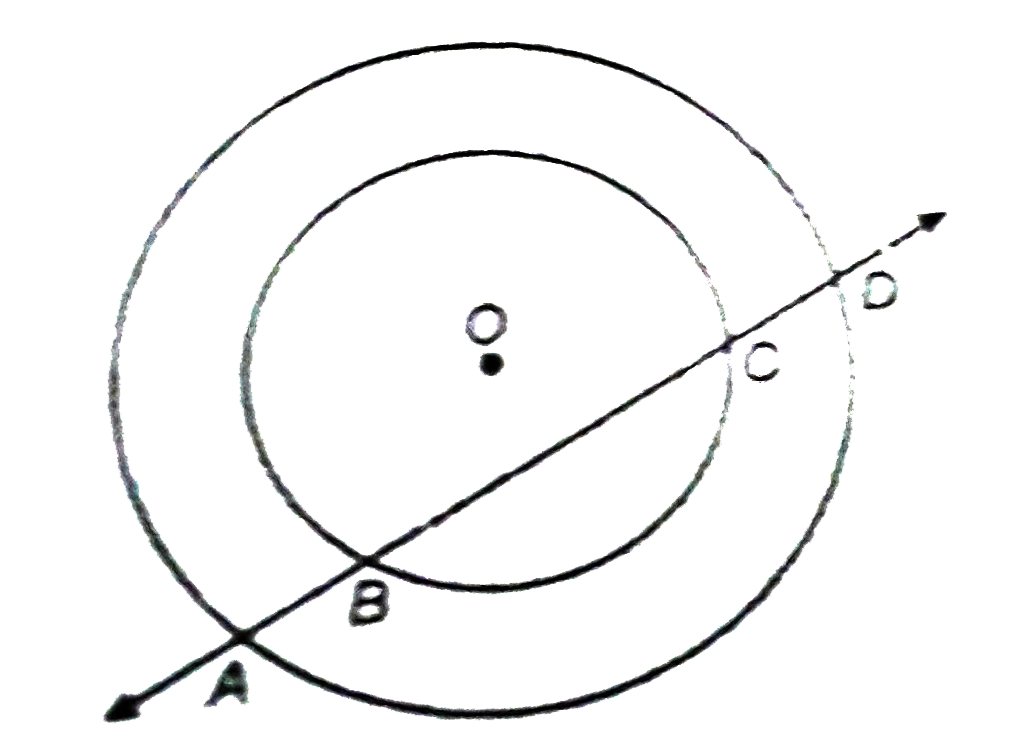 View Solution
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
 View Solution
View SolutionGiven two concetric circles with centre O. A line cut the circle at A,B,C and D respectively. If AB=10cm, then find the length of CD.
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
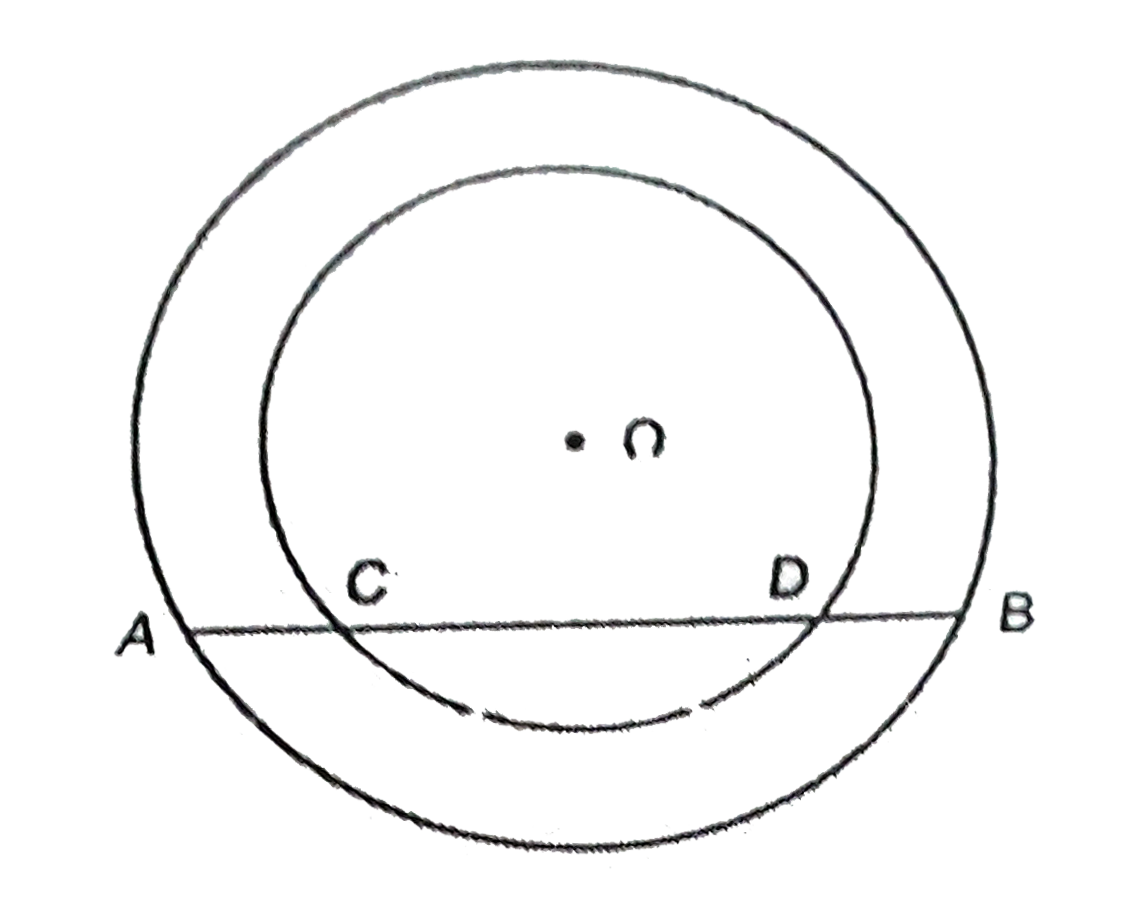 View Solution
View Solution


