If AOB is a diameter of the circle and AC=BC, then ∠CAB is equal to
30∘
60∘
90∘
45∘
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify the Given Information:
- AOB is the diameter of the circle.
- AC = BC (meaning the lengths of chords AC and BC are equal).
2. Draw the Circle:
- Draw a circle with center O.
- Mark points A and B on the circumference such that AOB is the diameter.
- Mark point C on the circumference such that AC = BC.
3. Use the Property of Isosceles Triangle:
- Since AC = BC, triangle ACB is isosceles.
- Therefore, angles opposite to equal sides are equal. This means:
∠CAB=∠CBA
- Let’s denote these angles as x. Thus, we have:
∠CAB=xand∠CBA=x
4. Use the Property of the Diameter:
- Since AOB is the diameter, angle ACB (the angle subtended by the diameter at the circumference) is a right angle:
∠ACB=90∘
5. Apply the Triangle Angle Sum Property:
- The sum of angles in triangle ACB is equal to 180 degrees:
∠CAB+∠CBA+∠ACB=180∘
- Substituting the known values:
x+x+90∘=180∘
- This simplifies to:
2x+90∘=180∘
6. Solve for x:
- Subtract 90 degrees from both sides:
2x=90∘
- Divide by 2:
x=45∘
7. Conclusion:
- Since x=∠CAB, we conclude that:
∠CAB=45∘
Final Answer:
∠CAB=45∘
---
- AOB is the diameter of the circle.
- AC = BC (meaning the lengths of chords AC and BC are equal).
- Draw a circle with center O.
- Mark points A and B on the circumference such that AOB is the diameter.
- Mark point C on the circumference such that AC = BC.
- Since AC = BC, triangle ACB is isosceles.
- Therefore, angles opposite to equal sides are equal. This means:
∠CAB=∠CBA
- Let’s denote these angles as x. Thus, we have:
∠CAB=xand∠CBA=x
- Since AOB is the diameter, angle ACB (the angle subtended by the diameter at the circumference) is a right angle:
∠ACB=90∘
- The sum of angles in triangle ACB is equal to 180 degrees:
∠CAB+∠CBA+∠ACB=180∘
- Substituting the known values:
x+x+90∘=180∘
- This simplifies to:
2x+90∘=180∘
- Subtract 90 degrees from both sides:
2x=90∘
- Divide by 2:
x=45∘
- Since x=∠CAB, we conclude that:
∠CAB=45∘
∠CAB=45∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
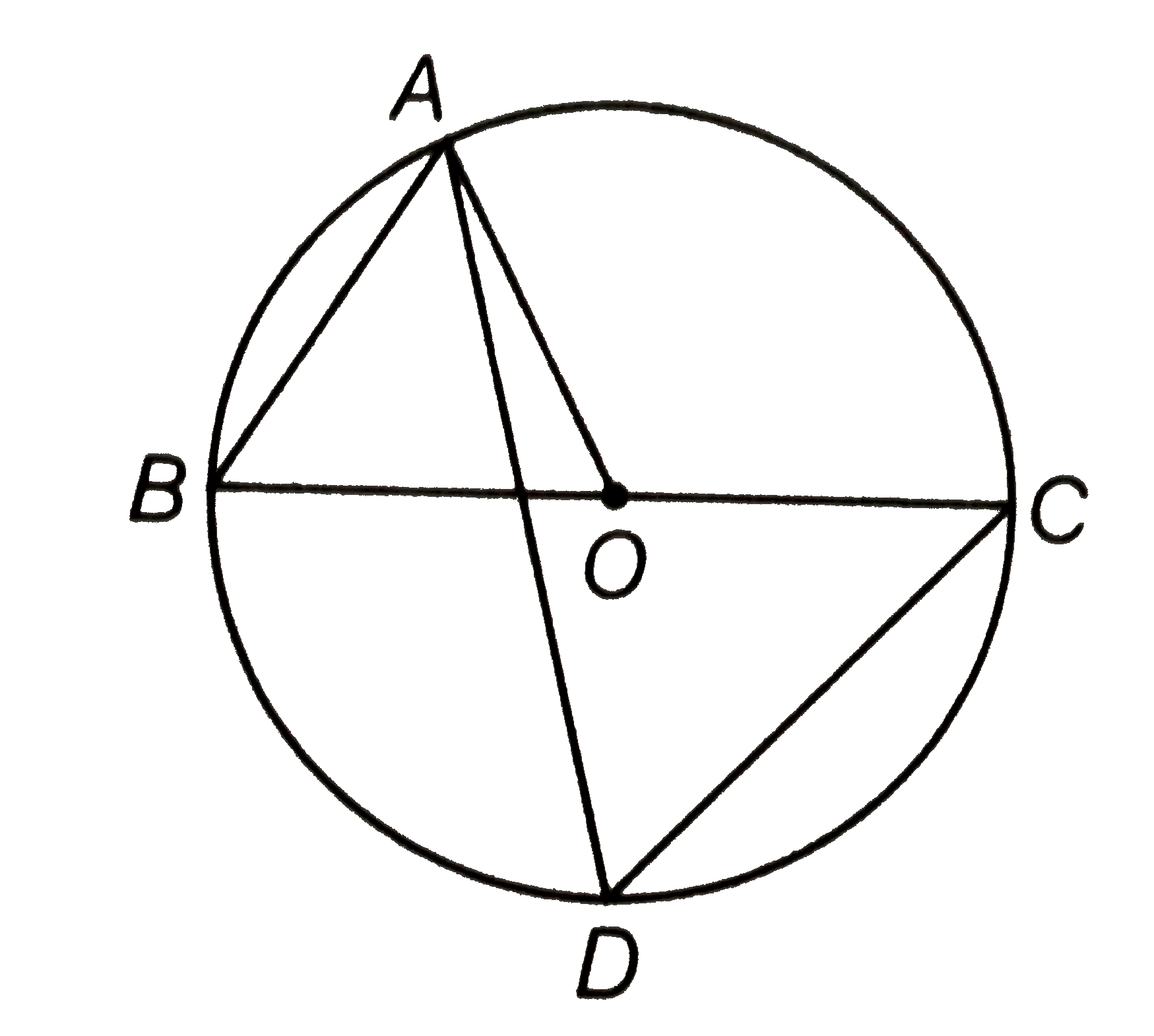
In figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
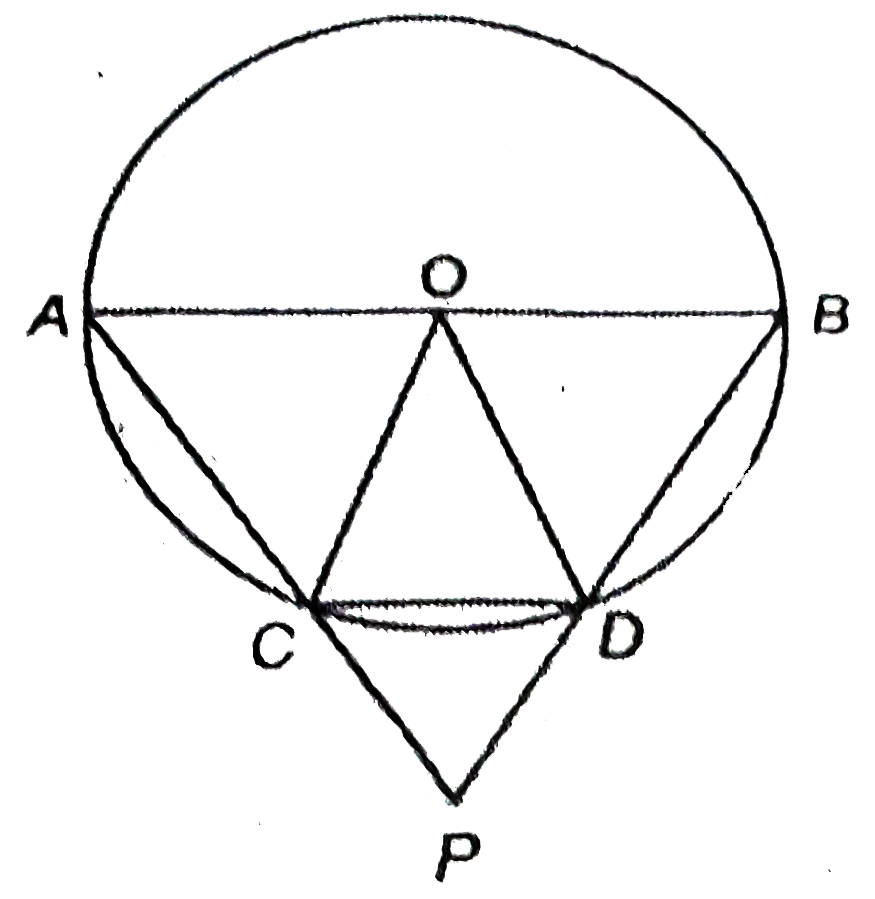
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
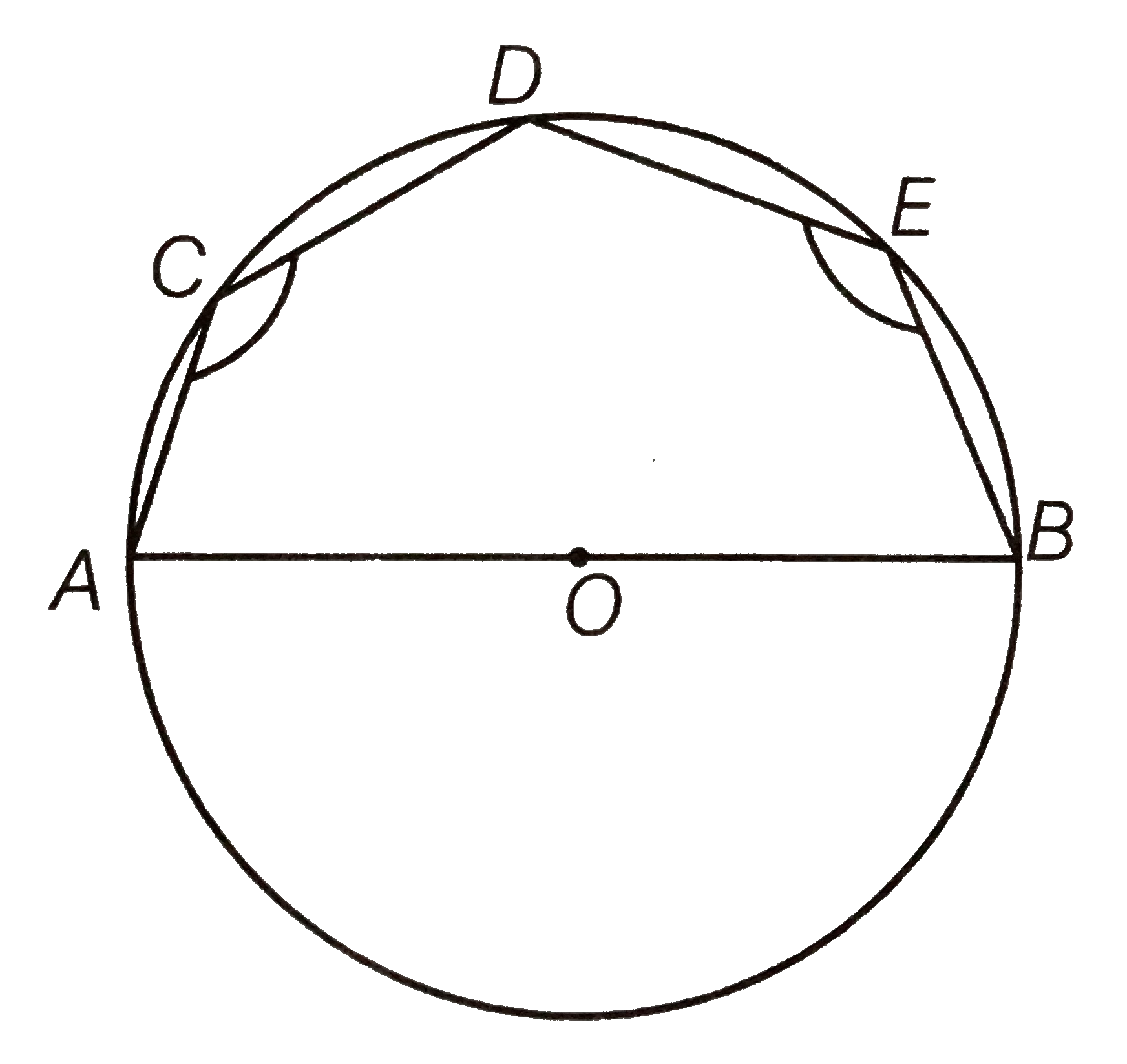
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View SolutionTriangle ABC is inscribed in a circle, such that AC is a diameter of the circle and angle BAC is 45∘. If the area of triangle ABC is 72 square units, how larger is the area of the circle than the area of triangle ABC ?
View SolutionIn the adjoining figure, AOB is the diameter of the circle. If ∠ABP=45∘, then find the value of ∠PQB.

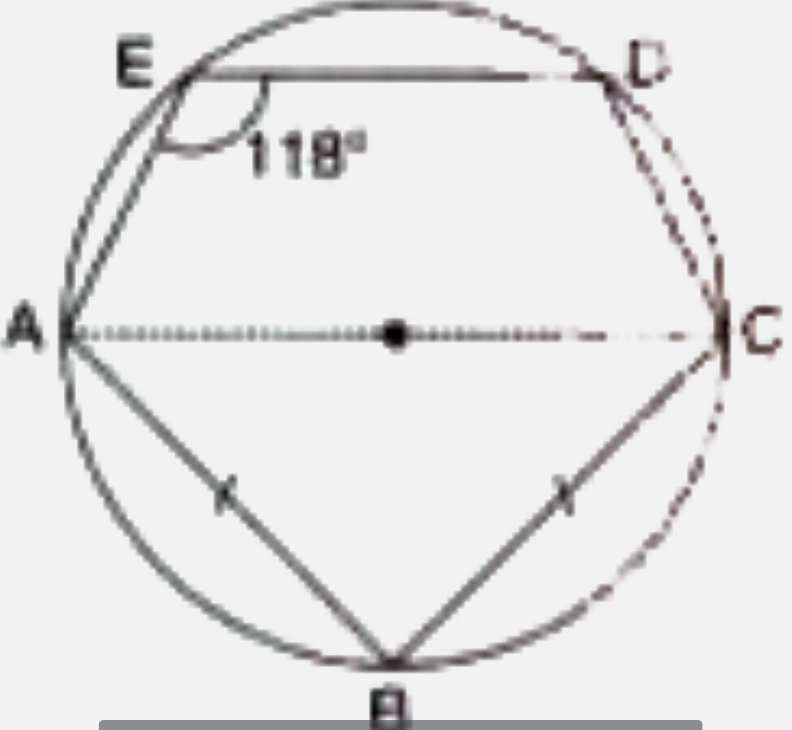
View SolutionIn the adjoining figure, AC is diameter of the circle AB = BC and ∠AED=118∘. Calculate :
∠DEC
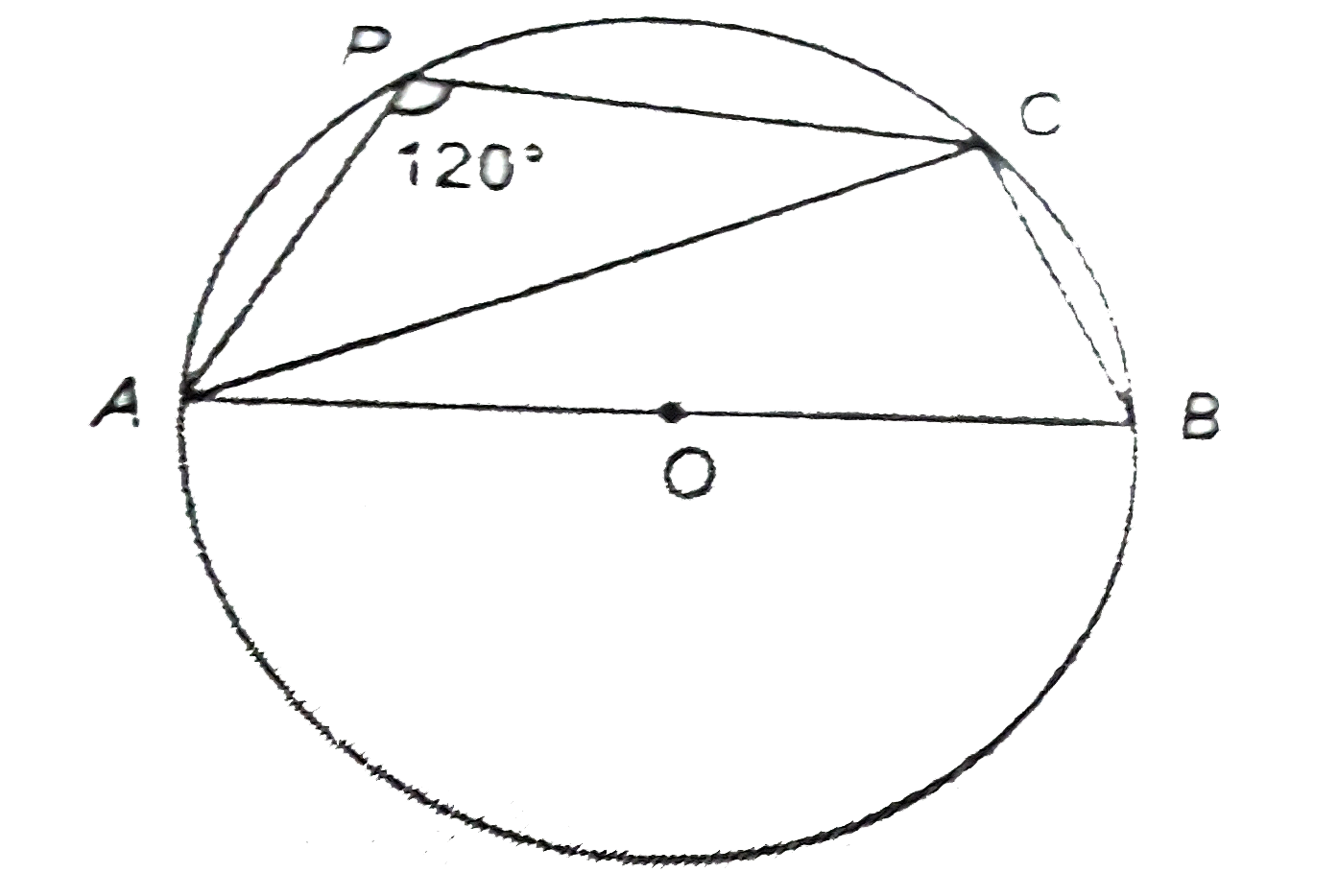
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View Solution
