If with ,then is equal to
The correct Answer is:A
To solve the problem, we need to find the ratio of the areas of triangles PRQ and BCA given that triangle ABC is similar to triangle PQR and that the ratio of the sides BC and QR is 1/3.
1. Understand the Similarity of Triangles:
Since ΔABC ~ ΔPQR, we know that the corresponding sides of similar triangles are in proportion.
2. Identify the Given Ratio:
We are given that BCQR=13.
3. Find the Ratio of QR to BC:
From the given ratio, we can find the inverse ratio:
QRBC=31
4. Use the Area Ratio Theorem:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(ΔPRQ)ar(ΔBCA)=(QRBC)2
5. Substitute the Ratio:
Now substitute the ratio we found in step 3 into the equation:
ar(ΔPRQ)ar(ΔBCA)=(31)2
6. Calculate the Square:
Calculate the square of the ratio:
ar(ΔPRQ)ar(ΔBCA)=91=9
Final Answer:
ar(ΔPRQ)ar(ΔBCA)=9
Since ΔABC ~ ΔPQR, we know that the corresponding sides of similar triangles are in proportion.
We are given that BCQR=13.
From the given ratio, we can find the inverse ratio:
QRBC=31
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can write:
ar(ΔPRQ)ar(ΔBCA)=(QRBC)2
Now substitute the ratio we found in step 3 into the equation:
ar(ΔPRQ)ar(ΔBCA)=(31)2
Calculate the square of the ratio:
ar(ΔPRQ)ar(ΔBCA)=91=9
ar(ΔPRQ)ar(ΔBCA)=9
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Short Answer Type Questions15videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
If in two ΔABC and ΔPQR, ABQR=BCPR=CAPQ, then
View SolutionIf ΔABC~ΔQRP,ar(ΔABC)ar(ΔPQR)=94,AB=18 cm and BC=15 cm, then PR is equal to
View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View SolutionIn a ΔABC,∠B=π3and∠C=π4 let D divide BC internally in the ratio 1:3, then sin(∠BAD)sin(∠CAD) is equal to :
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).
 View Solution
View SolutionThe value of Σnr=1(a+r+ar)(−a)r is equal to
View SolutionΔI1I2I3 is an excentral triangle of an equilateral triangle ΔABC such that I1I2=4 unit, if ΔDEF is pedal triangle of ΔABC, then Ar(ΔI1I2I3)Ar(ΔDEF)=
View SolutionThe eccentric angles of the vertices A,B,C of a triangle inscribed in the ellipse x242+y212=1 are α,β,γ. Let P,Q,R be the points on the auxiliary circle corresponding to points A,B,C respectively of the ellipse. ar(ΔPQR)ar(ΔABC)= (A) 2 (B) 4 (C) 9 (D) 26
View SolutionWhich of the following pairs of triangles are congruent ? Also state the condition of congruency in each case :

(iv) In ΔABC and ΔDEF,AB=EF,BC=DF and ∠B=∠F
(v) In ΔABC and ΔPQR,AB=QR,AC=PR and ∠B=∠R
(vi) In ΔABC and ΔPQR,∠A=∠P,AC=PR and AB=PQ
(vi) In ΔABC and ΔPQR,AB=QR,∠A=∠Q and AC=QP.View SolutionIn the given figure, DE // BC.
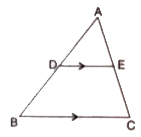
Given that AD=12BD, calculate DE, if BC = 45 cm.
Also , find Ar.(ΔADE)Ar.(ΔABC)andAr.(ΔADE)Ar.(trapezium BCED)View Solution

