Question

If each one of the following graphs is the graph of a polynomial, then
identify which one corresponds to a linear polynomial and which one
corresponds to a quadratic polynomial?  
(FIGURE)

Explanation

To identify which graphs correspond to linear and quadratic polynomials, we will analyze the characteristics of each graph based on their shapes.

Step 1: Analyze the first graph (y = f(x))
- Observation: The first graph is a parabola that opens upwards.
- Conclusion: Since it has a U-shape, it indicates that it is a quadratic polynomial. Quadratic polynomials can be expressed in the form \( ax^2 + bx + c \) where \( a \) is positive.

Step 2: Analyze the second graph (y = g(x))
- Observation: The second graph is a straight line.
- Conclusion: A straight line indicates that this is a linear polynomial. Linear polynomials can be expressed in the form \( mx + b \) where \( m \) is the slope.

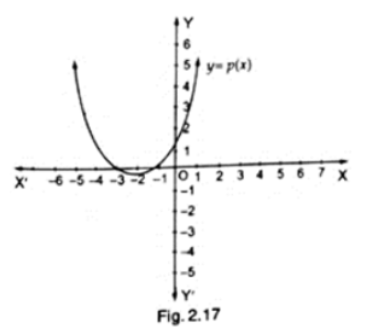
Step 3: Analyze the third graph (y = p(x))
- Observation: The third graph does not resemble a standard polynomial graph (it may be a curve or a different shape).
- Conclusion: This graph does not correspond to either a linear or a quadratic polynomial.

Step 4: Analyze the fourth graph (y = q(x))
- Observation: The fourth graph is a parabola that opens downwards.
- Conclusion: Similar to the first graph, this is also a quadratic polynomial, but with a negative coefficient for \( x^2 \), indicating it opens downwards.

Summary of Results:
1. The first graph (y = f(x)) is a quadratic polynomial.
2. The second graph (y = g(x)) is a linear polynomial.
3. The third graph (y = p(x)) is neither.
4. The fourth graph (y = q(x)) is a quadratic polynomial.