If function f has exactly two distinct real zeros, which of the following graphs could be the complete graph of f (x) ?




The correct Answer is:A
To solve the problem of identifying which graph could represent a function f(x) with exactly two distinct real zeros, we need to analyze the characteristics of the graphs provided. Here’s a step-by-step solution:
Step 1: Understand the concept of real zeros
Real zeros of a function f(x) are the points where the graph intersects the x-axis. If a function has exactly two distinct real zeros, it means the graph must touch or cross the x-axis at exactly two different points.
Hint: Look for points where the graph intersects the x-axis; these points represent the zeros of the function.
Step 2: Analyze the first graph
In the first graph, observe the points where the graph touches the x-axis. If the graph intersects the x-axis at two distinct points, then this graph could represent the function f(x).
Hint: Count the number of times the graph crosses or touches the x-axis.
Step 3: Analyze the second graph
In the second graph, check how many times the graph intersects the x-axis. If it touches the x-axis at three different points, then it has three distinct real zeros, which does not satisfy the condition of having exactly two distinct real zeros.
Hint: If the graph intersects the x-axis more than two times, it cannot be the correct option.
Step 4: Analyze the third graph
In the third graph, if the graph only touches the x-axis at one point, it indicates that there is only one real zero (with multiplicity). This does not meet the requirement of having two distinct real zeros.
Hint: A single touch at the x-axis indicates a repeated root, not distinct zeros.
Step 5: Analyze the fourth graph
In the fourth graph, if the graph intersects the x-axis at three points, similar to the second graph, it indicates three distinct real zeros. Therefore, this option is also not valid.
Hint: Again, look for the number of distinct intersections with the x-axis.
Conclusion
After analyzing all four graphs, the only graph that meets the requirement of having exactly two distinct real zeros is the first graph. Therefore, the answer is:
The complete graph of f(x) is represented by option one.
Real zeros of a function f(x) are the points where the graph intersects the x-axis. If a function has exactly two distinct real zeros, it means the graph must touch or cross the x-axis at exactly two different points.
In the first graph, observe the points where the graph touches the x-axis. If the graph intersects the x-axis at two distinct points, then this graph could represent the function f(x).
In the second graph, check how many times the graph intersects the x-axis. If it touches the x-axis at three different points, then it has three distinct real zeros, which does not satisfy the condition of having exactly two distinct real zeros.
In the third graph, if the graph only touches the x-axis at one point, it indicates that there is only one real zero (with multiplicity). This does not meet the requirement of having two distinct real zeros.
In the fourth graph, if the graph intersects the x-axis at three points, similar to the second graph, it indicates three distinct real zeros. Therefore, this option is also not valid.
After analyzing all four graphs, the only graph that meets the requirement of having exactly two distinct real zeros is the first graph. Therefore, the answer is:
Topper's Solved these Questions
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - EXPONENTS
1 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - POLYNOMIALS
1 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - RATIONAL EXPRESSIONS AND EQUATIONS
1 Videos
- ANSWERING SAT READING QUESTIONS BOOK - KAPLANCHAPTER - ANSWERING SAT READING QUESTIONS EXERCISE - TRY ON YOUR OWN
22 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Videos
Similar Questions
Knowledge Check
Which of the following graphs could not be the graph of a function?
A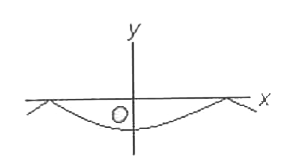 B
B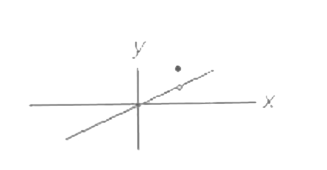 C
C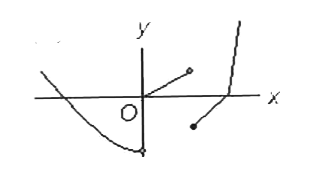 D
D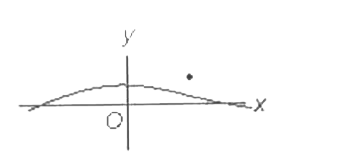
12 If the function f has five distinct zeros, which of the following could represent the complete graph of f in the xy‑plane?
A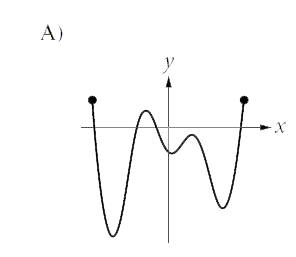 B
B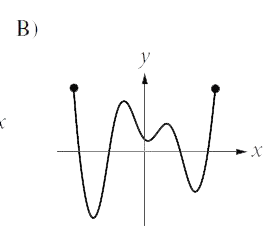 C
C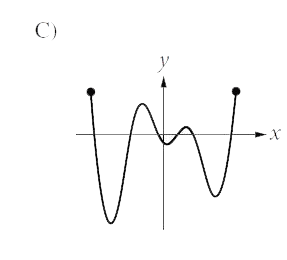 D
D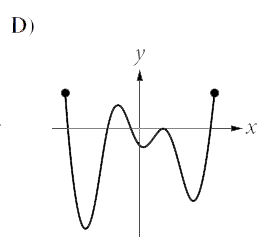
If a function p(x) has four distinct zeros, which of the following could represent the entire graph of p in a standard coordinate plane?
A B
B C
C D
D
The range of the polynomial function f is the set of real numbers less than or equal to 4. If the zeros of f are −3 and 1, which of the following could be the graph of y = f (x) in the xy-plane?
View SolutionIf in the quadratic function f(x)=ax2+bx+c, a and c are both negative constant, which of the following could be the graph of function f?
View Solution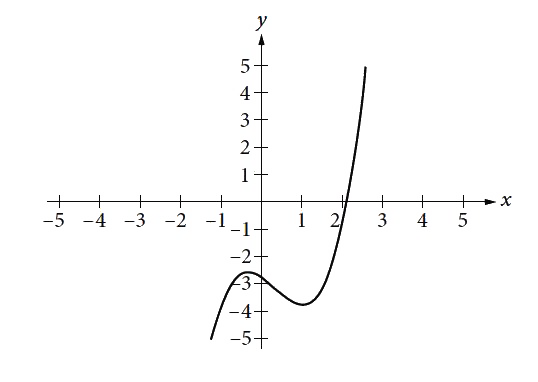
The function f(x)=x3−x2−x−114 s graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k ?
View SolutionThe graph of y=f(x) is shown below.
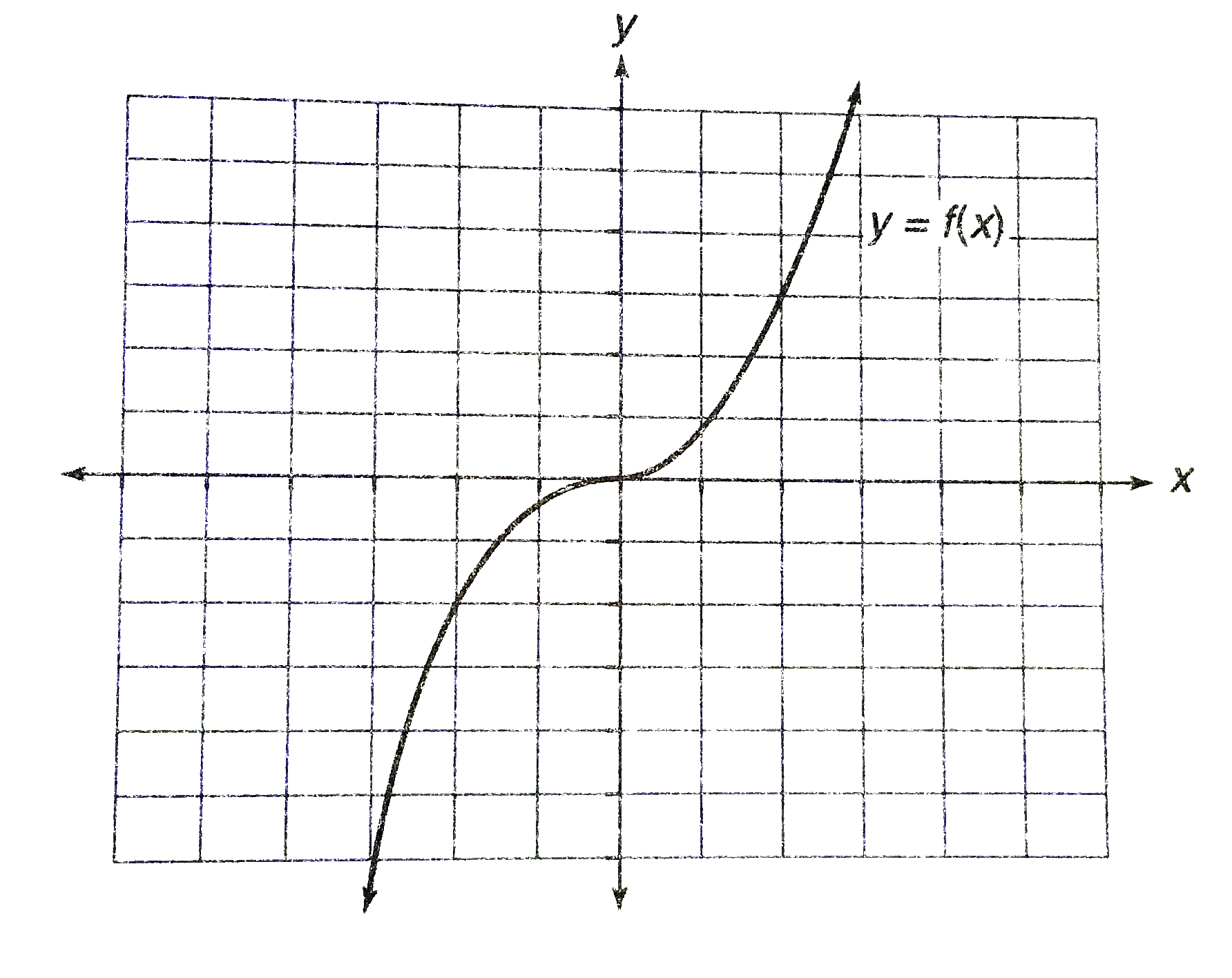
Which of the following could represents the graph of y=f(x−2)+1?
View SolutionIf f(x)=4x+2, which of the following is the graph of f(x)?
View Solution
