If f(x) = sec 2x + cosec 2x, then f(x) is discontinuous at all points in Solution in Punjabi
A. {nπ,n∈N}
B. {(2n±1)π4,n∈I}
C. {nπ4,n∈I}
D. {(2n±1)π8,n∈I}
The correct Answer is:A, B, C
Step by step video & image solution for If f(x) = sec 2x + cosec 2x, then f(x) is discontinuous at all points in by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)11videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 43videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)50videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 83videos
COMPLEX NUMBERS
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.08:34View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
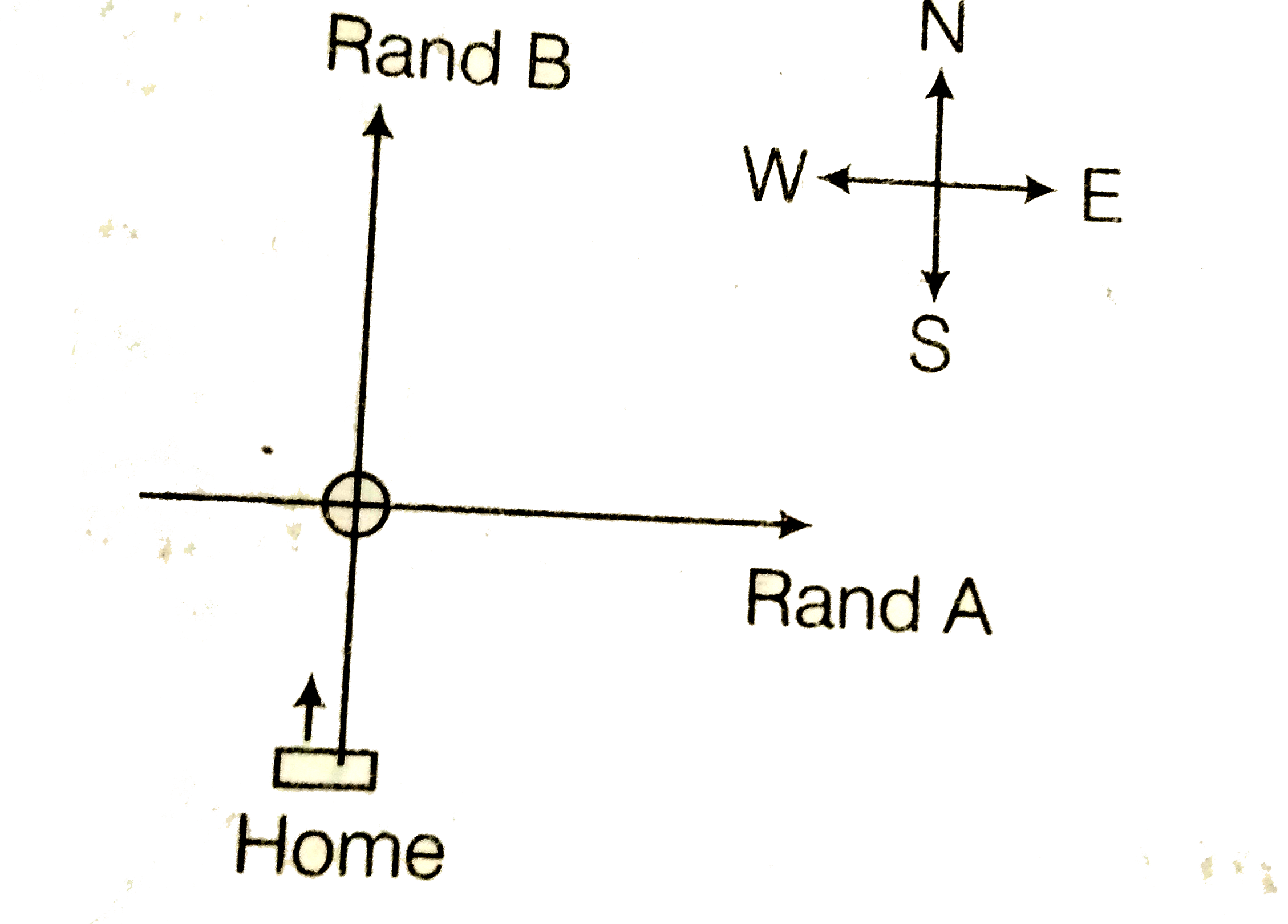
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous06:51View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
02:49View SolutionFind the modules of 2+3ι
03:54View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
06:19View SolutionFind all points of discontinuity of f, where f is defined byf(x)={2x+3ifx≤22x−3ifx>2
09:09View Solutionf(x)=|(secx,cos x,sec^2x + cot x cosecx),(cos^2x,cos^2x,cosec^2 x),(1,cos^2x,cos^2x)| then int_0^(pi/2) f(x) dx=.....
08:02View SolutionIf f(x) = sec 2x + cosec 2x, then f(x) is discontinuous at all points in
08:34View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):} .
08:50View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):} .
09:09View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):} .
View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):} .
06:34View SolutionFind all points of discontinuity of f, where f is defined by f(x) = {{:(2x+3," if "x le 2),(2x-3," if "x gt 2):} .
04:37View Solutionf(x)=∣∣ ∣ ∣∣secxcosxsec2x+cotxcosecxcos2xcos2xcosec2x1cos2xcos2x∣∣ ∣ ∣∣ then ∫π20f(x)dx=.....
02:23View SolutionFind all points of discontinuity of f, where f is defined by f(x)={2x+3,ifx≤22x−3,if x>2
02:23View Solutionमाना f(x)=2 cosec 2x+secx+cosec x है, तो x∈(0,π2) के लिए f(x) का न्यूनतम मान है
01:39View Solution

