If f(x)={(−x=π2,x≤−π2),(−cosx,−π2<x,≤0),( x-1, 0 lt x le 1),("in"x, x gt1):} Solution in Punjabi
f(x) is continuous at x=−π2
f(x) is not differentiable at x = 0
f(x) is differentiable at x = 1
All of the above
The correct Answer is:A, B, C, D
Step by step video & image solution for If f(x) ={{:(-x=(pi)/(2),xle -(pi)/(2)), (- cos x, -(pi)/(2)lt x ,le 0):},( x-1, 0 lt x le 1),("in"x, x gt1):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Statement I And Ii Type Questions)11videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 43videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Single Option Correct Type Questions)50videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - ARIHANT MATHSCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 83videos
COMPLEX NUMBERS
- BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
Similar Questions
Statement I f(x)=sinx+[x] is discontinuous at x = 0.
Statement II If g(x) is continuous and f(x) is discontinuous, then g(x) + f(x) will necessarily be discontinuous at x = a.04:27View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
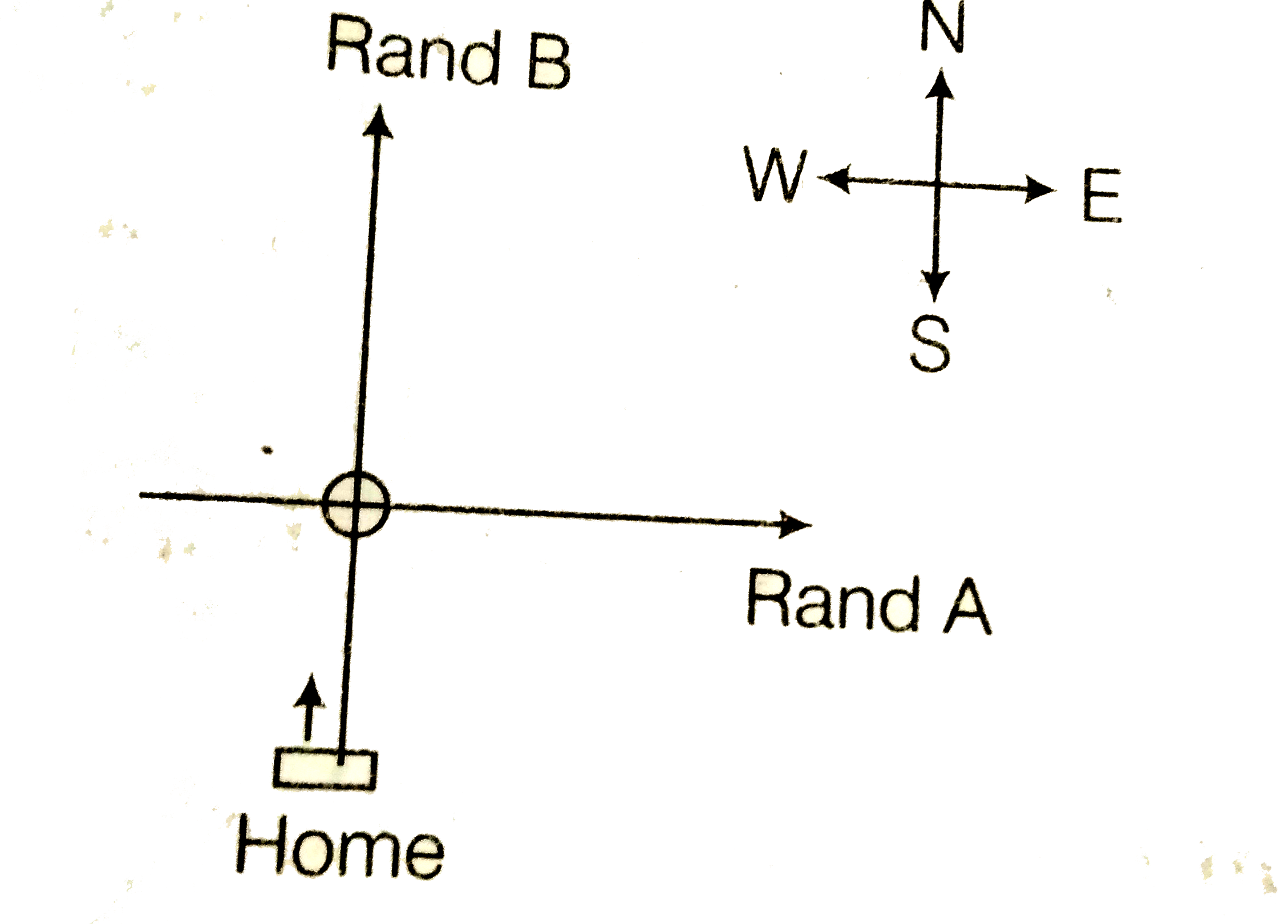
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Now if roads A and B are taken as X-axis and y-axis ,then visible point representing the graph of y=f(x)
Then the value of x at which function f(x) is discontinous03:14View SolutionIf f(x)={sinπx2,x<1[x],x≥1, where [x] denotes the greatest integer function, then
View SolutionFind the modules of 2+3ι
02:53View SolutionIf a vertex of a triangle is (1, 1) and the mid-points of two side through this vertex are (-1, 2) and (3, 2), then centroid of the triangle is
01:50View SolutionIf f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩−x−π2 , x≤−π2−cosx , −π2<x≤0,thenx−1, 0<x≤1lnx, x>1
01:22View SolutionIf f(x)={1x<01+sinx0≤x<π2 then derivative of f(x) x=0
03:12View Solutionयदि f(x)={(−x−π2,,x≤−π2),(−cosx,,−π2<x≤0,),(x−1,0<x≤1) तब-
03:34View SolutionLet f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinxfor−π≤x≤−π2asinx+bfor−π2<x<π2cosxforπ2≤x≤π. If f is continuous on [−π,π), then find the values of a and b.
04:46View Solution(f(x)=cosxandH1(x)=min{f(t),0≤t<x},),(0≤x≤π2=π2−x,π2<x≤π),(f(x)=cosxandH2(x)=max{f(t),o≤t≤x},),(0≤x≤π2=π2−x,π2<x≤π),(g(x)=sinxandH3(x)=min{g(t),0≤t≤x},),(0≤x≤π2=π2−x,π2≤x≤π),(g(x)=sinxandH4(x)=max{g(t),0≤t≤x},),(0≤x≤π2=π2−x,π2<x≤π)
Which of the following is true for H2(x)?10:22View Solution(f(x)=cosxandH1(x)=min{f(t),0≤t<x},),(0≤x≤π2=π2−x,π2<x≤π),(f(x)=cosxandH2(x)=max{f(t),o≤t≤x},),(0≤x≤π2=π2−x,π2<x≤π),(g(x)=sinxandH3(x)=min{g(t),0≤t≤x},),(0≤x≤π2=π2−x,π2≤x≤π),(g(x)=sinxandH4(x)=max{g(t),0≤t≤x},),(0≤x≤π2=π2−x,π2<x≤π)
Which of the following is true for H4(x)?03:43View SolutionIf f(x)=⎧⎨⎩sin2x√1−cos2x, for 0<x≤π2cosxπ−2x, for π2<x≤π
04:18View SolutionLet f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤π then f(x) has
08:10View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
03:56View Solutionमाना फलन f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩sgn(x)+x−∞<x<0−1+sinx0≤x<π2cosxπ2≤x<∞ है। बिंदु x=0 तथा x=π2 पर संततता तथा अवकलनीयता की जाँच कीजिये।
03:57View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩3−x+1for−1≤x<0tan(x/2)for0≤x≤πxx2−2forπ≤x≤6, then √f(0)+f(π/6)+15f(5)−123=……………..
05:14View Solution

