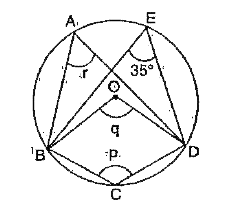
If O is the centre of a circle, find the value of x in each of the following figures :
Video Solution
Text Solution
(i) ∠BDC=∠BAC=30∘[Δ in the same segment]
In ΔBCD, the sum of the angles is 180∘.
∴∠CBD+∠BCD+∠BDC=180∘
⇒70∘+x∘+30∘=180∘
⇒x=80∘
(ii) ∠APB=90∘[ angle in a semicircle ].
∠BAP+∠APB+∠ABP=180∘
⇒∠BAP+90∘+35∘=180∘
⇒∠BAP=(180∘−125∘)=55∘
Now, x∘∠BQP=∠BAP=55∘ [ Δ in the same segment].
Hence, x=55.
(ii) OA = OB ⇒∠OAB⇒OBA=25∘
OC = OA ⇒∠OAC=∠OCA=35∘
∴∠BAC=∠OAB+∠OAC=(25∘+35∘)=60∘
Now, x∘=∠BOC=2∠BAC=(2×60∘)=120∘
∴x=120
(iv) We know that the sum of all angles at a point is 360∘.
∴90∘+120∘+∠BOC=360∘⇒∠BOC=150∘
∠BOC=2∠BAC⇒2x=150⇒x=75
(v) ∠ODB⇒∠OAC=50∘ [ angles in the same segment]
OB= OD ⇒∠OBD=∠ODB=50−x∘
⇒x=50.
(vi) Reflex ∠AOC=(360∘−130∘)=230∘
∴∠ABC=12×reflex ∠AOC=(12×230∘)=115∘=x∘
∴x=115
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
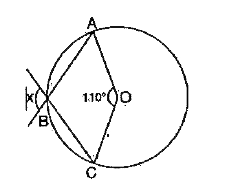 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In fig. O is Centre of circle, find x∘
View SolutionIn the figure , in a circle with centre O, length of chord AB is equal to the radius of the circle. Find the measure of each of the following :
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB

View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
View SolutionIn each of the following figures, find the values of x and y

View SolutionIn the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
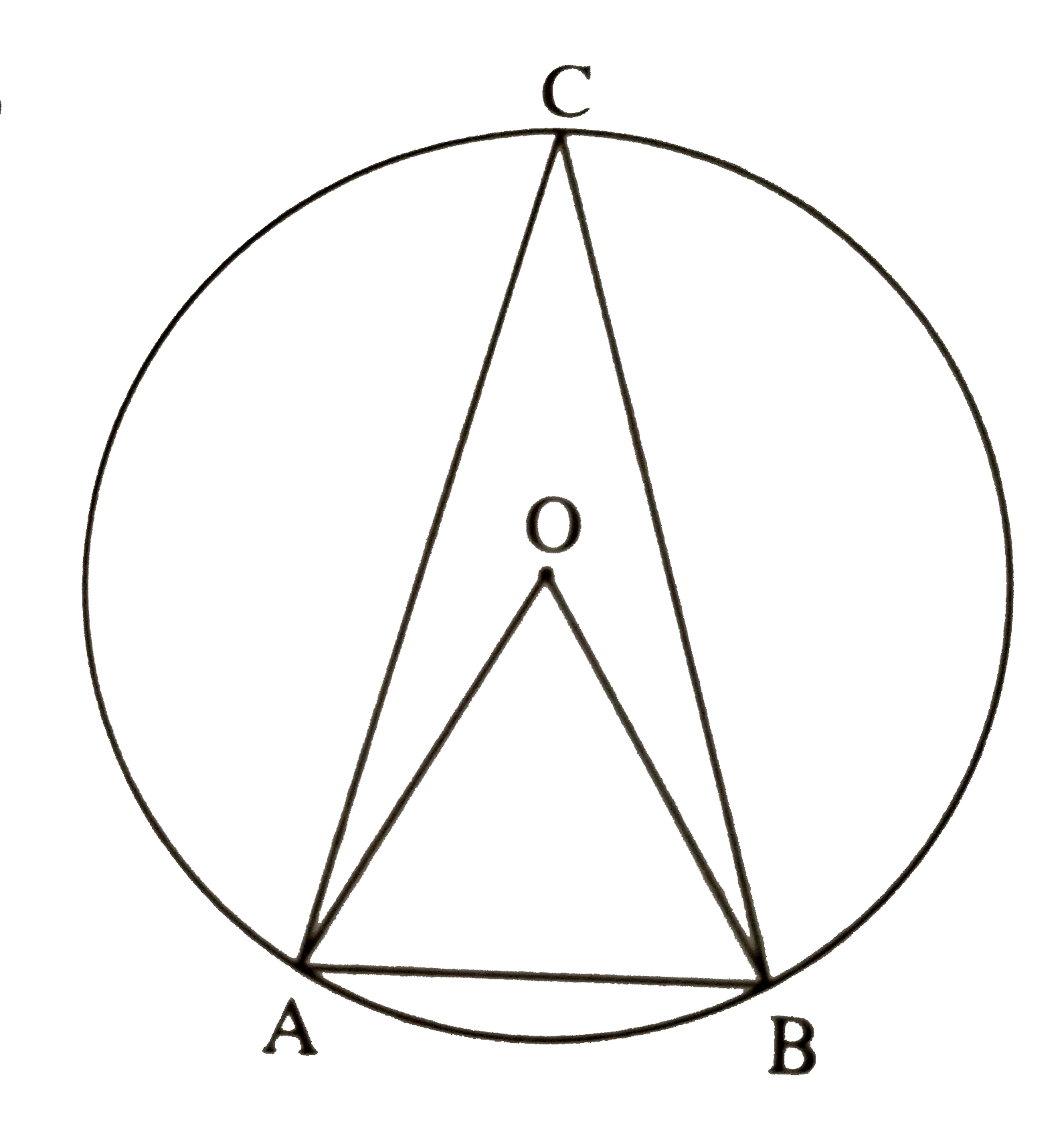
View Solution