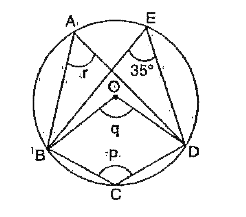
If O is the centre of the circle , find the value of x in eaxh of the following figures.
Video Solution
Text Solution
(i) In ΔADC, we have
∠CAD+∠ADC+∠ACD=180∘
⇒50∘+90∘+∠ACD=180∘
⇒∠ACD=40∘
But, ∠ACD=90∘ [angle in a semicircle] .
∴∠ACD+x∘=90∘
⇒40∘+x∘=90∘
⇒x=50
(ii) Since AOB is a straight line , we have
∠AOC+∠BOC=180∘
⇒130∘+∠BOC=180∘
⇒∠BOC=180∘−130∘=50∘
Now, ∠DBC=12∠BOC=25∘⇒x=25
(iii) ∠BDC=∠BAC=40∘ [ Δ in the same segment ].
∠BDC+∠DBC+∠BCD=180∘
∴40∘+80∘+x∘=180∘⇒x=60
(iv) OA= OC ⇒∠OCA=∠OAC=50∘
Side CO of ΔOCA is produced to B.
∴ ext. ∠AOB=∠OAC+∠OCA=(50∘+50∘)=100
Now, ∠BDA=12∠AOB=(12×100∘)=50∘
Henc, x=50
(v) In Δ OBA, we have OA =OB.
∴∠OBA=∠OAB=50∘⇒∠CBA=50∘
Now, ∠CDA=x∘=∠CBA=50∘=50∘[Δ in the same segment ].
∴x=50.
(vi)OA=OB [ each equal to the radius of the circle ]
⇒∠OBA=∠OAB=x∘
∴x∘+x∘+40∘=180∘⇒2x∘=140∘⇒x=70.
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
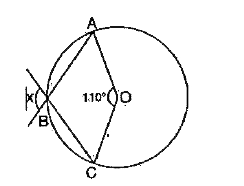 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn fig. O is Centre of circle, find x∘
View SolutionIn Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
View SolutionIn Figure, O is the centre of the circle. If ∠CEA=300, find the values of x, y and z
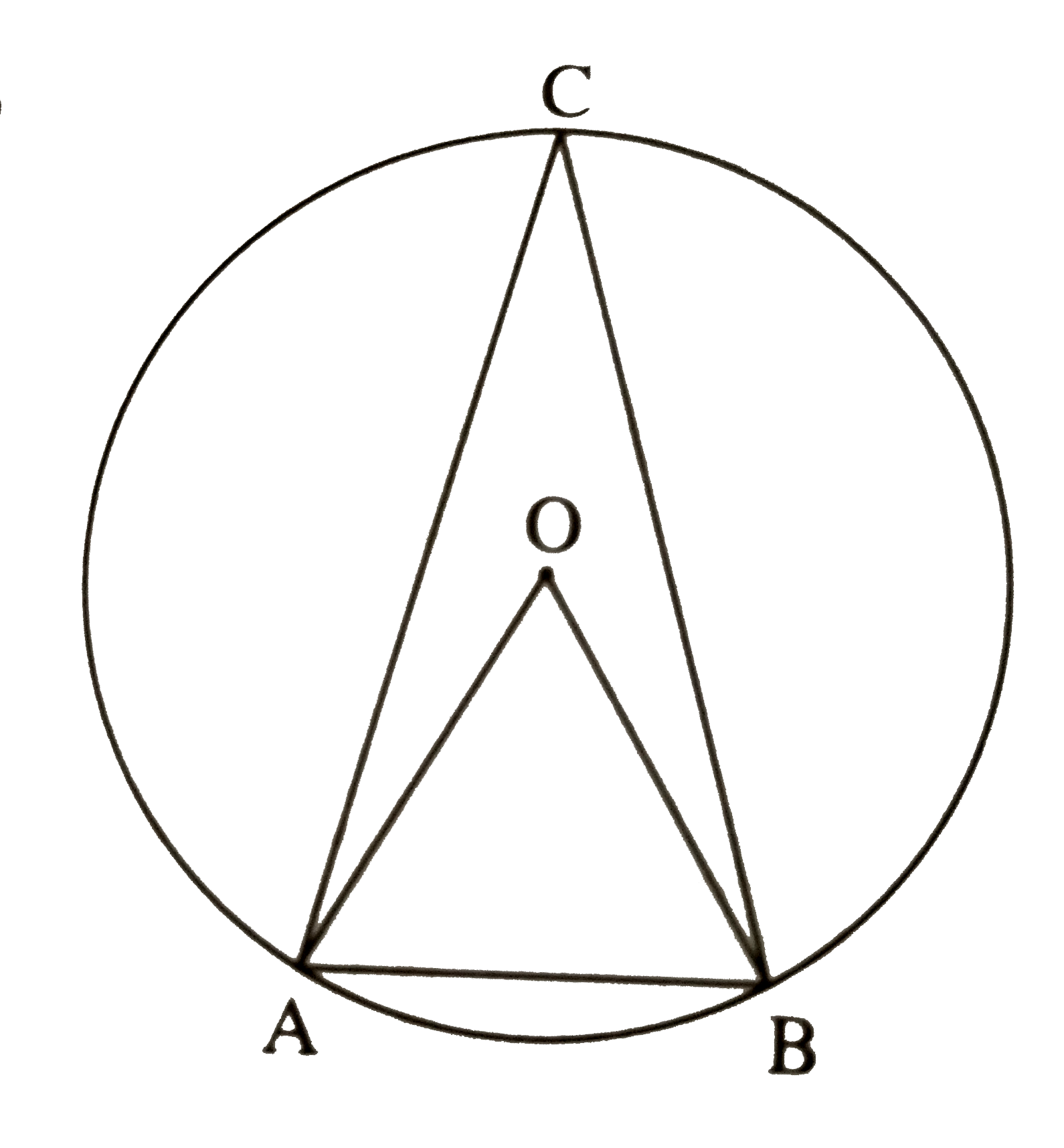
View SolutionIn the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
View SolutionIn given figure, O is the centre of the circle.
Which of the following is not the radius of the given circle?
View Solution