If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
Given: A cyclic quadrilateral ABCD. Side AB is produced to E
To prove: ∠CBE=∠ADC
Proof : ∠ABC+∠ADC=180∘ .......... (i)
Sum of opposite pairs of angles in a cyclic quadrilateral is equal to 180∘
But ∠ABC+∠CBE=180∘ ............. (ii)[∠ABC and ∠CBE are linear pairs]
From (i) and (ii),
∠ABC+∠ADC=∠ABC+∠CBE
∠ADC=∠CBE or ∠CBE=∠ADC
Hence proved.
Topper's Solved these Questions
Similar Questions
If a side of the cyclic quadrlateral is produced ; then the external angle is equal to the interior opposite angles.
View SolutionTHEOREM (Exterior Angle Property of a Triangle) : If a side of a triangle is produced the exterior angle so formed is equal to the sum of two interior opposite angles.
View Solution
Knowledge Check
- Question 1 - Select One
one side of a triangle is produced and the exterior angle so formed is 140∘. If the interior opposite angles are in the ratio. 2:5, find the measure of each angle of the triangle.
A40∘,75∘,60∘B40∘,70∘,70∘C40∘,100∘,40∘D40∘,75∘,65∘ - Question 2 - Select One
If an exterior angle of a cyclic quadrilateral be 50∘, then the opposite interior angle is :
A130∘B40∘C50∘D90∘ - Question 3 - Select One
If an exterior angle of a cyclic quadrilateral be 50∘, then the opposite interior angle is :
A130∘B40∘C50∘D90∘
Theorem 6.8 : If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
View SolutionExterior angle theorem : If a side of a triangle is produced; the exterior angle so formed is equal to the sum of the two interior opposite angles.
View Solutionone side of a triangle is produced and the exterior angle so formed is 120∘.if the interior opposite angles be in the ratio 3:5.find the measure of each angles of triangle .
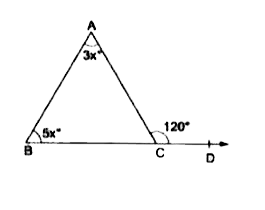 View Solution
View SolutionIf the exterior angle of a quadrilateral formed by producing one of its sides is equal to the interior opposite angle, prove that the quadrilateral is cyclic.
View Solution27.Prove that an exterior angle of a triangle is equal to the sum of its interior opposite angles.
View Solution

