If S is the sum of possible values of c for which the area of the figure bounded by the curves y=s∈2x, the straight lines x=π6,x=c, and the abscissa axis is equal to 12, then the value of π/S is____
The correct Answer is:6
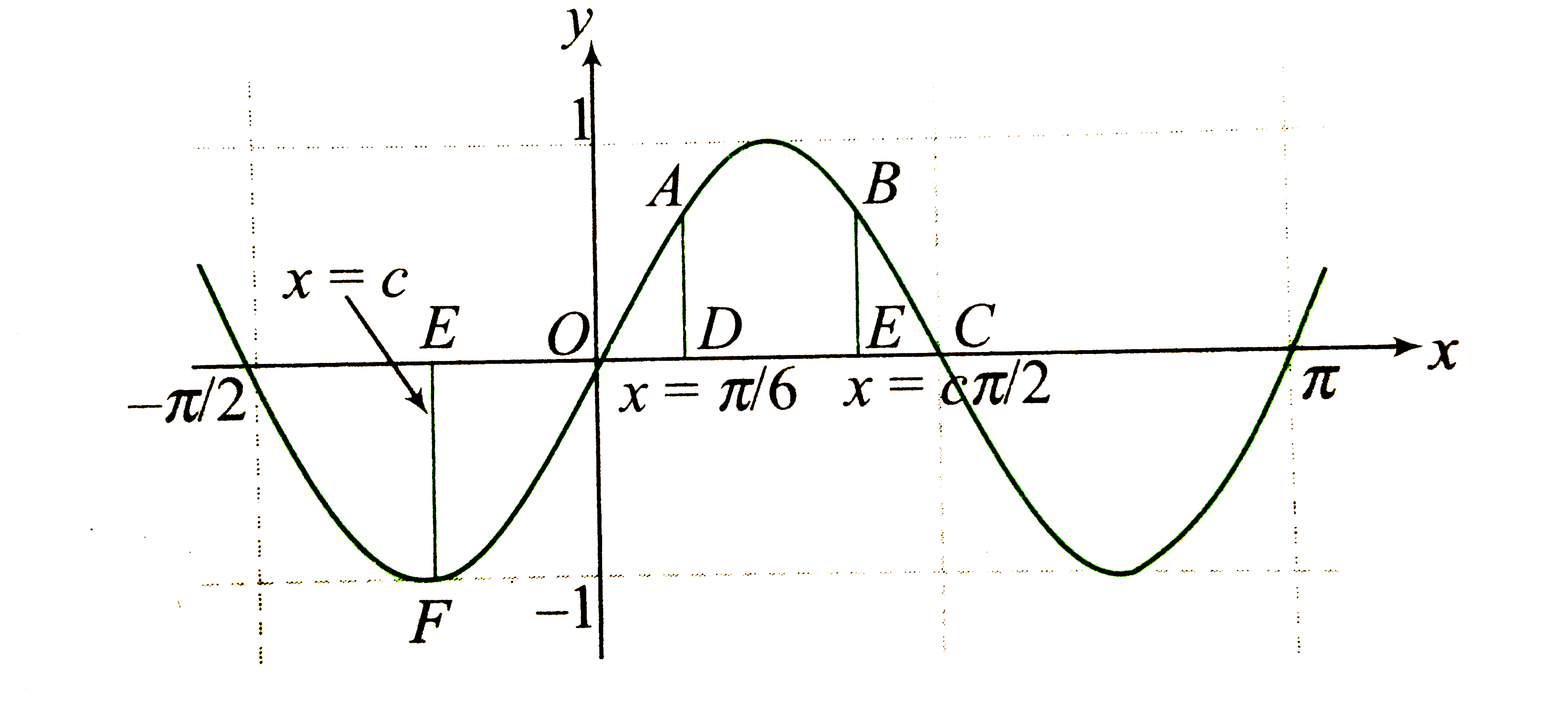
Area OABC=π/2∫0sin2xdx=1
Area OAD=π/6∫0sin2xdx=14
Since sin 2x is symmetric about origin,
so c=−π6, because areaOAD= area OEF
c∫π6sin2xdx=12
cos2c=−12cos2c=32 (not posible)
c=π3
so c=−π3,π3
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
If S is the sum of possible values of c for which the area of the figure bounded by the curves y=s∈2x, the straight lines x=π6,x=c, and the abscissa axis is equal to 12, then the value of π/S is____
View SolutionIf S is the sum of cubes of possible value of c for which the area of the figure bounded by the curve y=8x2−x5, then straight lines x=1andx=c and the abscissa axis is equal to 163, then the value of [S],where[.] denotest the greatest integer function, is____
View Solution
Knowledge Check
Which of the following is the possible value/values of c for which the area of the figure bounded by the curves y=sin2x, the straight lines x=π/6,x=c and the abscissa axis is equal to 1/2?
A−π6Bπ3Cπ6Dnone of theseFind the value of ‘c’ for which the area of the figure bounded by the curve, y=8x2–x5, the straight lines x = 1 and x = c and the abscissa axis is equal to 16/3.
A2B√8−√17C3DnoneThe value of a for which the area of the region bounded by the curve y=sin2x, the straight lines x=π/6,x=a and x-axis is equal to 1/2 is-
Aπ/2Bπ/3C4/3Dπ/6
Find the area of the figure bounded by the curve y=sin−1x, the lines x=0 and y=π2.
View SolutionFind the value of ‘c’ for which the area of the figure bounded by the curve, y=8x2–x5, the straight lines x = 1 and x = c and the abscissa axis is equal to 16/3.
View SolutionFind the area bounded by the curves y=|sinx|, the x-axis and the lines |x|=π.
View SolutionThe value of k for which the area of the figure bounded by the curve y=8x2−x5, the straight line x=1 and x=k and the x-axis is equal to 16/3
View SolutionThe area of the region bounded by the curve y = sin x between the ordinates x=0,x=π2 and the X-axis is
View Solution
