If the bisector of the vertical angle of a triangle bisects the base of the triangle;then the triangle is iscsceless.
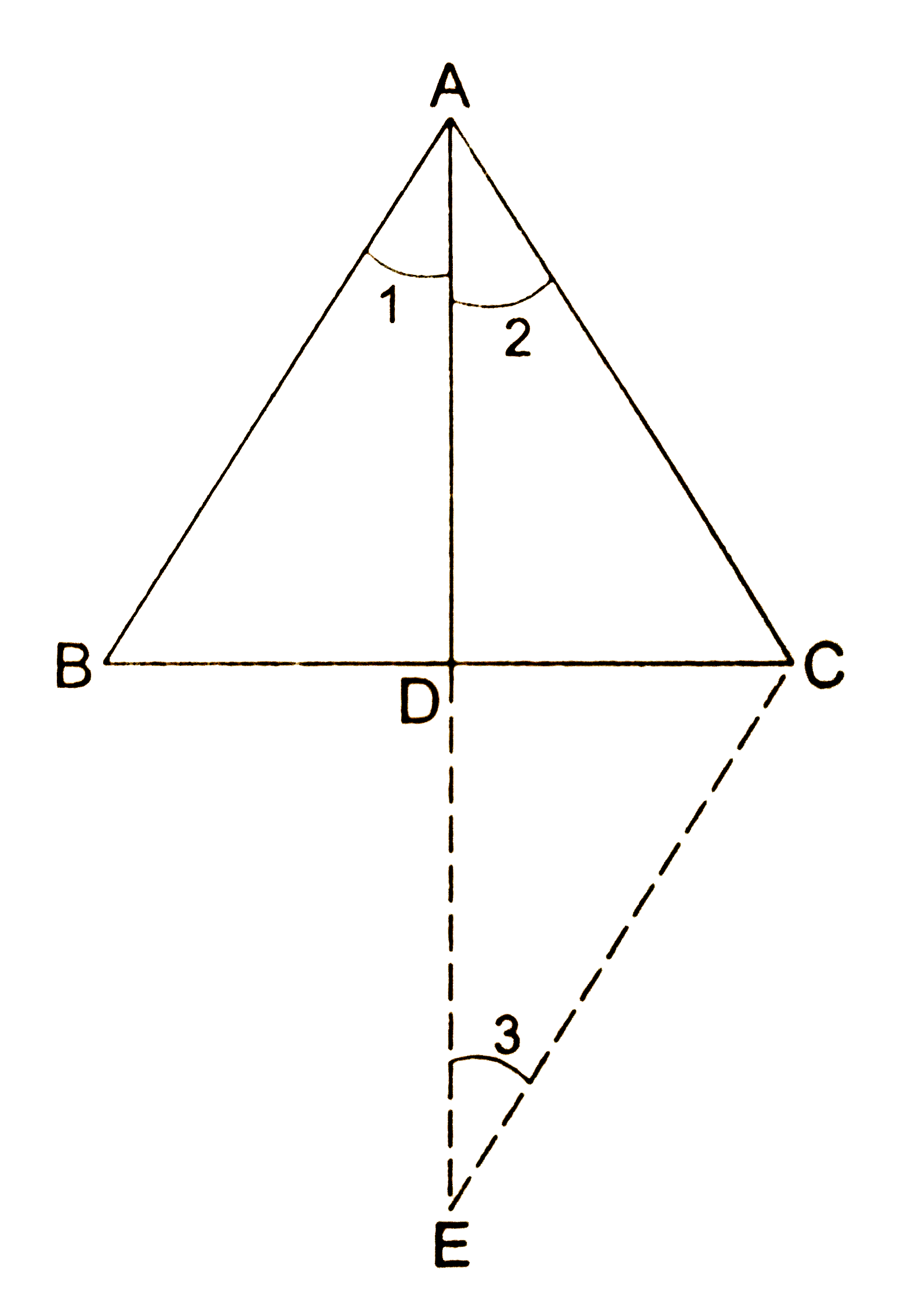
Given A ΔABC in which AD is the bisector of ∠A, which meets BC in D such that BD = DC.
TO PROVE AB = AC.
CONSTRUCTION Produce AD to E such that AD = DE.
Joint EC.
PROOF In ΔABDandΔECD, we have
BD = DC (given),
AD = DE (by construction),
∠ADB=∠EDC (vert. opp.∠s).
∴ ΔABD≅ΔECD (SAS-criteria).
∴ AB=ECand∠1=∠3 (c.p.c.t.).
Also, ∠1=∠2 [∵AD bisects ∠A]
∴ ∠2=∠3.
But, we know that the sides opposite to equal angles of a triangle are equal.
∴ EC=AC.
So, AB=AC [∵EC=AB].
Hence, ΔABC is isosceles.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
If the bisector of the vertical angle of a triangle bisects the base of the triangle;then the triangle is isosceles.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A ABC in which AD is the bisector of ∠A meeting BC in D such that BD=DC.
View Solution
Knowledge Check
If the straight line which bisects the vertical angle of a triangle is perpendicular to the base, the triangle is:
AequilateralBisoscelesCscaleneDright- angled
If the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionJoinA→D
Hence,AD∥BC
∠ACB=∠CAD(alternateangle
∠BAC=∠ACD(alternateangle)
HenceAB=AC (by ASA congurency )so, it is isosceles triangle.
View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View SolutionProve that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionShow that the bisector of vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View Solution
