If x−2y+4=0and2x+y−5=0 are the sides of an isosceles triangle having area 10sq.units , the equation of the third side is 3x−y=−9 (b) 3x−y+11=0 x−3y=19 (d) 3x−y+15=0
x+3y=-1
x+3y=19
3x-y=-9
3x-y=11
The correct Answer is:A, B, C, D
Given lines are mutually perpendicular and intersect at A(65,135).
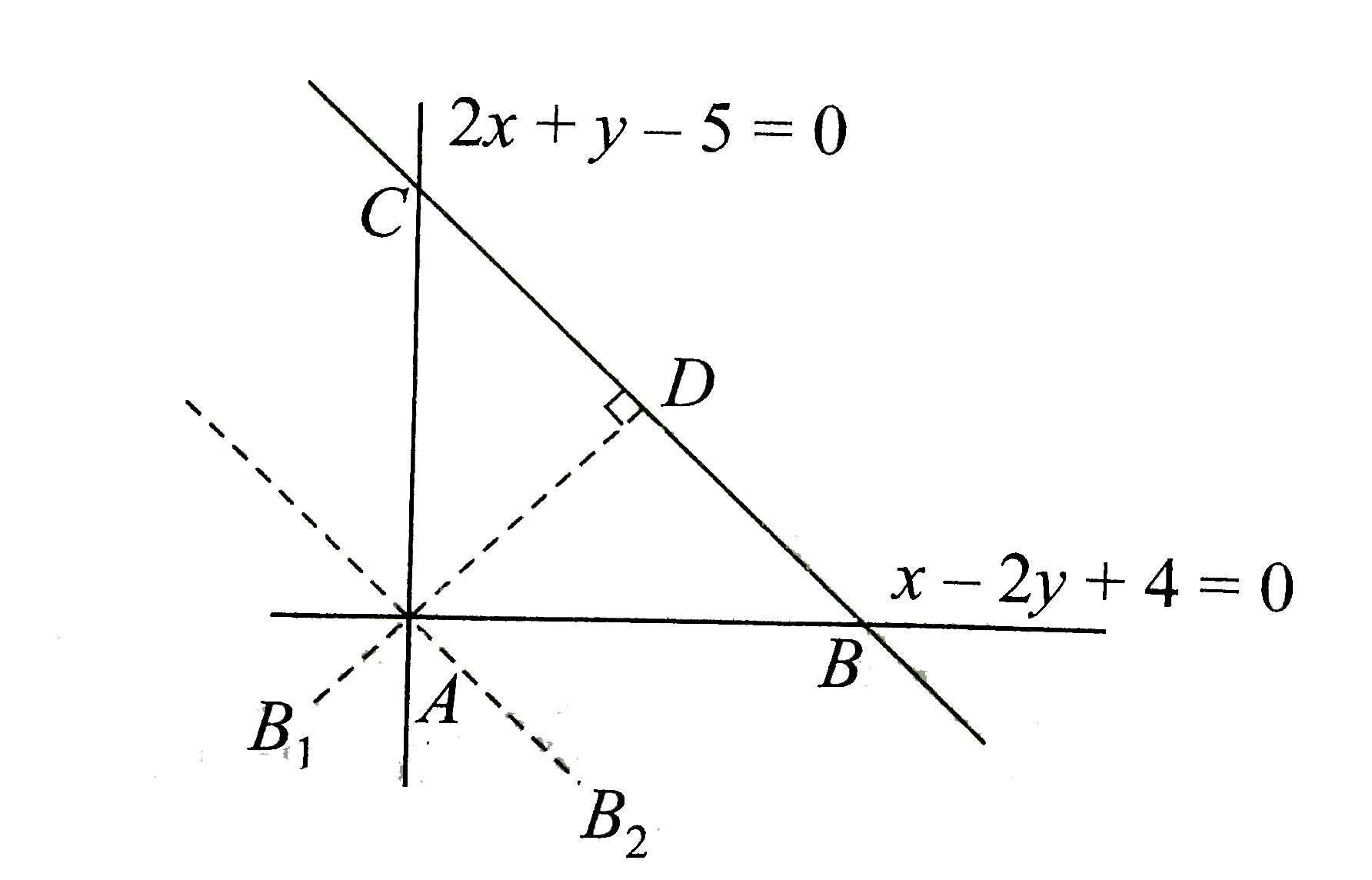
Equation of angle bisectors B1 and B2 of the given lines are
x−2y+4=±(2x+y−5)
or x+3y=9 and 3x-y=1
Side BC will be parallel to these bisectors
Let AD = a.
∴AB=a√2
Area of triangle ABC=12×(a√2)2=a2
∴a2=10 (Given)
or a=√10
Let equations of BC be x+3y=λ.Then
√10=∣∣185−135−λ∣∣√10
λ=−9,11
Therefore, equation of BC is 3x-y=-9 or 3x-y = 11
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Matrix)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Single)
Explore 82 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
If x−2y+4=0and2x+y−5=0 are the sides of an isosceles triangle having area 10sq.units , the equation of the third side is (a) 3x−y=−9 (b) 3x−y+11=0 (c) x−3y=19 (d) 3x−y+15=0
View SolutionTwo equal sides of an isosceles triangle are given by the equations 7x−y+3=0 and x+y−3=0. The slope of the third side is
View SolutionTwo equal sides of an isosceles triangle are 7x−y+3=0,x−y−3=0 and its third side passes through the point (1,0) the equation of the third side is (A) 3x+y+7=0 (B) x−3y+29=0 (C) 3x+y+3=0 (D) 3x+y−3=0
View Solutionx + 8y -22=0, 5x +2y-34 =0, 2x - 3y +13 = 0 are the three sides of a triangle.The area of the triangle is
View Solution. If 2x2−5xy+2y2=0 represents two sides of triangle whose centroid is (1, 1) then the equation of the third side is (A) x+y−3=0 (B) x−y−3=0 (C) x+y+3=0 (D) x−y+3=0
View SolutionIf the lines x+y=0,x−y=0and2x+3y=6=0 are the sides of a triangle and (−2,a) is an interior point of the triangle then a lies
View SolutionThe extremities of the base of an isosceles triangle are (2,0)and(0,2) . If the equation of one of the equal side is x=2, then the equation of other equal side is x+y=2 (b) x−y+2=0 y=2 (d) 2x+y=2
View SolutionThe equations of two sides of a triangle are 3x−2y+6=0 and 4x+5y−20 and the orthocentre is (1,1). Find the equation of the third side.
View SolutionFind the area of the triangle, the equations of whose sides are y=x, y=2x and y-3x=4.
View SolutionTwo equal sides of an isosceles triangle are given by equations 7x−y+3=0 and x+y−3=0. It's third side passes through the point (1,−10). Determine the equation of the third side. (A)x−3y−31=0 (B) 3x+y+7=0 (C) Both (A), (B) (D) Neither (A), nor (B)
View Solution
